
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A在y轴的正半轴上,点C在x轴的正半轴上,线段OA,OC的长分别是m,n且满足(m-6)2+![]() =0,点D是线段OC上一点,将△AOD沿直线AD翻折,点O落在矩形对角线AC上的点E处
=0,点D是线段OC上一点,将△AOD沿直线AD翻折,点O落在矩形对角线AC上的点E处

(1)求线段OD的长
(2)求点E的坐标
(3)DE所在直线与AB相交于点M,点N在x轴的正半轴上,以M、A、N、C为顶点的四边形是平行四边形时,求N点坐
【答案】(1)OD=3;(2)E点(![]() ,
,![]() )(3)点N为(
)(3)点N为(![]() ,0)或(
,0)或(![]() ,0)
,0)
【解析】
(1)根据非负性即可求出OA,OC;根据勾股定理得出OD长;
(2)由三角形面积求法可得![]() ,进而求出EG和DG,即可解答;
,进而求出EG和DG,即可解答;
(3)由待定系数法求出DE的解析式,进而求出M点坐标,再利用平行四边形的性质解答即可.
解:(1)∵线段OA,OC的长分别是m,n且满足![]()
∴OA=m=6,OC=n=8;
设DE=x,由翻折的性质可得:OA=AE=6,OD=DE=x,DC=8-OD=8-x,
![]() =10,
=10,
可得:EC=10-AE=10-6=4,
在Rt△DEC中,由勾股定理可得:DE2+EC2=DC2,
即x2+42=(8-x)2,
解得:x=3,
可得:DE=OD=3,
(2)过E作EG⊥OC,

在Rt△DEC中,
![]() ,
,
即![]()
解得:EG=![]() ,
,
在Rt△DEG中,![]() ,
,
∴OG=3+![]() =
=![]() ,
,
所以点E的坐标为(![]() ,
,![]() ),
),
(3)
设直线DE的解析式为:y=ax+c,把D(3,0),E(4.8,2.4)代入解析式可得:
 ,
,
解得: ,
,
所以DE的解析式为:![]() ,
,
把y=6代入DE的解析式![]() ,可得:x=
,可得:x=![]() ,
,
即AM=![]() ,
,
当以M、A、N、C为顶点的四边形是平行四边形时,
CN=AM=![]() ,
,
所以ON=8+![]() =
=![]() ,ON'=8-
,ON'=8-![]() =
=![]() ,
,
即存在点N,且点N的坐标为(![]() ,0)或(
,0)或(![]() ,0).
,0).


科目:初中数学 来源: 题型:
【题目】如图,DB∥AC,且DB=![]() AC,E是AC的中点.
AC,E是AC的中点.

(1)求证:四边形BDEC是平行四边形;
(2)连接AD、BE,△ABC添加一个条件: ,使四边形DBEA是矩形(不需说明理由).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在Rt△ABC中,∠C=90°,AC=9,BC=12,点 D、E 分别在边AC、BC上,且CD:CE=3︰4.将△CDE绕点D顺时针旋转,当点C落在线段DE上的点 F处时,BF恰好是∠ABC的平分线,此时线段CD的长是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个三角形数阵,仔细观察排列规律:
第1行 1
第2行 -![]()
![]()
第3行 -![]()
![]() -
-![]()
第4行 ![]() -
-![]()
![]() -
-![]()
.....
按照这个规律继续排列下去,第21行第2个数是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校实施新课程改革以来,学生的学习能力有了很大提高,王老师为进一步了解本班学生自主学习、合作交流的现状,对该班部分学生进行调查,把调查结果分成四类(A:特别好,B:好,C:一般,D:较差)后,再将调查结果绘制成两幅不完整的统计图(如图①②).请根据统计图解答下列问题:
(1)本次调查中,王老师一共调查了________名学生;
(2)将条形统计图补充完整;
(3)为了共同进步,王老师从被调查的A类和D类学生中分别选取一名学生进行“兵教兵”互助学习,请用列表或画树状图的方法求出恰好选中一名男生和一名女生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】河南省旅游资源丰富,2013~2017年旅游收入不断增长,同比增速分别为:15.3%,12.7%,15.3%,14.5%,17.1%.关于这组数据,下列说法正确的是( )
A. 中位数是12.7% B. 众数是15.3%
C. 平均数是15.98% D. 方差是0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半径为1个单位的圆片上有一点Q与数轴上的原点重合.(提示:圆的周长C=2πr,结果保留π的形式)
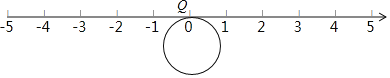
(1)把圆片沿数轴向右滚动1周,点Q到达数轴上点A的位置,点A表示的数是 ;
(2)圆片在数轴上向右滚动的周数记为正数,圆片在数轴上向左滚动的周数记为负数,依次运动情况记录如下:+2,﹣1,+3,﹣5,﹣1
①第几次滚动后,Q点距离原点最远?
②当圆片结束运动时,Q点运动的路程共有多少?此时点Q所表示的数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:如图1,等腰△ABC中,AB=AC,∠BAC=120°,作AD⊥BC于点D,则D为BC的中点,∠BAD=![]() ∠BAC=60°,于是
∠BAC=60°,于是![]() =
=![]() ;
;
迁移应用:如图2,△ABC和△ADE都是等腰三角形,∠BAC=∠ADE=120°,D,E,C三点在同一条直线上,连接BD.
①求证:△ADB≌△AEC;
②请直接写出线段AD,BD,CD之间的等量关系式;
拓展延伸:如图3,在菱形ABCD中,∠ABC=120°,在∠ABC内作射线BM,作点C关于BM的对称点E,连接AE并延长交BM于点F,连接CE,CF.
①证明△CEF是等边三角形;
②若AE=5,CE=2,求BF的长。



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】涡阳某童装专卖店在销售中发现,一款童装每件进价为![]() 元,销售价为
元,销售价为![]() 元时,每天可售出
元时,每天可售出![]() 件,为了迎接“六-一”儿童节,商店决定采取适当的降价措施,以扩大销售增加利润,经市场调查发现,如果每件童装降价
件,为了迎接“六-一”儿童节,商店决定采取适当的降价措施,以扩大销售增加利润,经市场调查发现,如果每件童装降价![]() 元,那么平均可多售出
元,那么平均可多售出![]() 件.
件.
(1)若每件童装降价![]() 元,每天可售出 件,每件盈利 元(用含
元,每天可售出 件,每件盈利 元(用含![]() 的代数式表示);
的代数式表示);
![]() 每件童装降价多少元时,能让利于顾客并且商家平均每天能赢利
每件童装降价多少元时,能让利于顾客并且商家平均每天能赢利![]() 元.
元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com