练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

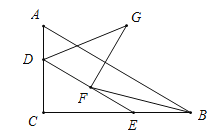
    【题目】已知，在Rt△ABC中，∠C=90°，AC=9，BC=12，点 D、E 分别在边AC、BC上，且CD:CE=3︰4．将△CDE绕点D顺时针旋转，当点C落在线段DE上的点 F处时，BF恰好是∠ABC的平分线，此时线段CD的长是________.

    【答案】6

    【解析】分析：设CD=3x，则CE=4x，BE=12﹣4x，依据∠EBF=∠EFB，可得EF=BE=12﹣4x，由旋转可得DF=CD=3x，再根据Rt△DCE中，CD2+CE2=DE2，即可得到（3x）2+（4x）2=（3x+12﹣4x）2，进而得出CD=6．

    详解：如图所示，设CD=3x，则CE=4x，BE=12﹣4x．∵=，∠DCE=∠ACB=90°，∴△ACB∽△DCE，∴∠DEC=∠ABC，∴AB∥DE，∴∠ABF=∠BFE．又∵BF平分∠ABC，∴∠ABF=∠CBF，∴∠EBF=∠EFB，∴EF=BE=12﹣4x，由旋转可得DF=CD=3x．在Rt△DCE中，∵CD2+CE2=DE2，∴（3x）2+（4x）2=（3x+12﹣4x）2，解得x1=2，x2=﹣3（舍去），∴CD=2×3=6．故答案为：6．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

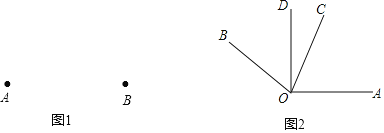
    【题目】（1）已知：点A和点B（如图1），根据条件画图（用三角板和量角器）：

    ①画射线BA；

    ②画∠ABC＝90°，使得点C在线段AB上方且AB＝BC；

    ③连接AC，画出∠ABC的角平分线BD，交AC于D．通过观察、度量、猜想获得线段BD、AC的关系．

    （2）已知：如图2，∠AOB＝150，OC平分∠AOB，AO⊥DO，求∠COD的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，四边形ABCD为平行四边形，∠BAD的角平分线AE交CD于点F，交BC的延长线于点E．

    （1）求证：BE=CD；

    （2）连接BF，若BF⊥AE，∠BEA=60°，AB=4，求平行四边形ABCD的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知平面直角坐标系（如图），直线的经过点和点.

    （1）求、的值；

    （2）如果抛物线经过点、，该抛物线的顶点为点，求的值；

    （3）设点在直线上，且在第一象限内，直线与轴的交点为点，如果，求点的坐标.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】植树节期间，市团委组织部分中学的团员去东岸湿地公园植树．三亚市第二中学七（3）班团支部领到一批树苗，若每人植4棵树，还剩37棵；若每人植6棵树，则最后一人有树植，但不足3棵，这批树苗共有_____棵．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线l1：y=﹣x+3与x轴相交于点A，直线l2：y=kx+b经过点（3，﹣1），与x轴交于点B（6，0），与y轴交于点C，与直线l1相交于点D．

    （1）求直线l2的函数关系式；

    （2）点P是l2上的一点，若△ABP的面积等于△ABD的面积的2倍，求点P的坐标；

    （3）设点Q的坐标为（m，3），是否存在m的值使得QA+QB最小？若存在，请求出点Q的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知直线y＝+1与x轴、y轴分别交于点A、B，以线AB为直角边在第一象限内作等腰Rt△ABC，∠BAC=90o、点P(x、y)为线段BC上一个动点(点P不与B、C重合)，设△OPA的面积为S。

    （1）求点C的坐标;

    （2）求S关于x的函数解析式，并写出x的的取值范围;

    （3）△OPA的面积能于吗，如果能，求出此时点P坐标，如果不能，说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，矩形OABC的顶点A在y轴的正半轴上，点C在x轴的正半轴上，线段OA,OC的长分别是m，n且满足(m-6)2+＝0，点D是线段OC上一点，将△AOD沿直线AD翻折，点O落在矩形对角线AC上的点E处

    （1）求线段OD的长

    （2）求点E的坐标

    （3）DE所在直线与AB相交于点M，点N在x轴的正半轴上，以M、A、N、C为顶点的四边形是平行四边形时，求N点坐

    查看答案和解析>>

    科目：初中数学 来源： 题型：

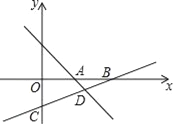
    【题目】如图，直线l1的解析式为y=﹣x+2，l1与x轴交于点B，直线l2经过点D（0，5），与直线l1交于点C（﹣1，m），且与x轴交于点A,

    （1）求点C的坐标及直线l2的解析式；

    （2）求△ABC的面积．

    查看答案和解析>>

    同步练习册答案