
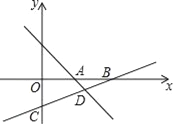
【题目】如图,直线l1:y=﹣x+3与x轴相交于点A,直线l2:y=kx+b经过点(3,﹣1),与x轴交于点B(6,0),与y轴交于点C,与直线l1相交于点D.
(1)求直线l2的函数关系式;
(2)点P是l2上的一点,若△ABP的面积等于△ABD的面积的2倍,求点P的坐标;
(3)设点Q的坐标为(m,3),是否存在m的值使得QA+QB最小?若存在,请求出点Q的坐标;若不存在,请说明理由.
【答案】(1)直线l2的函数关系式为:y=![]() x﹣2;
x﹣2;
(2)点P的坐标为(![]() ,
, ![]() )或(
)或(![]() ,
, ![]() );
);
(3)存在m的值使得QA+QB最小,此时点Q的坐标为(![]() ,3).
,3).
【解析】试题分析: (1)把点(3,﹣1),点B(6,0)代入直线l2,求出k、b的值即可;
(2)设点P的坐标为(t, ![]() t﹣2),求出D点坐标,再由S△ABP=2S△ABD求出t的值即可;
t﹣2),求出D点坐标,再由S△ABP=2S△ABD求出t的值即可;
(3)作直线y=3,作点A关于直线y=3的对称点A′,连结A′B,利用待定系数法求出其解析式,根据点Q(m,3)在直线A′B上求出m的值,进而可得出结论.
试题解析:
(1)由题知: ![]()
解得:  ,
,
故直线l2的函数关系式为:y=![]() x﹣2;
x﹣2;
(2)由题及(1)可设点P的坐标为(t, ![]() t﹣2).
t﹣2).
解方程组 ,得
,得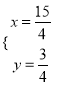 ,
,
∴点D的坐标为(![]() ,﹣
,﹣![]() ).
).
∵S△ABP=2S△ABD,
∴![]() AB|
AB|![]() t﹣2|=2×
t﹣2|=2×![]() AB|﹣
AB|﹣![]() |,即|
|,即|![]() t﹣2|=
t﹣2|=![]() ,解得:t=
,解得:t=![]() 或t=
或t=![]() ,
,
∴点P的坐标为(![]() ,
, ![]() )或(
)或(![]() ,
, ![]() );
);
(3)作直线y=3(如图),再作点A关于直线y=3的对称点A′,连结A′B.

由几何知识可知:A′B与直线y=3的交点即为QA+QB最小时的点Q.
∵点A(3,0),
∴A′(3,6)
∵点B(6,0),
∴直线A′B的函数表达式为y=﹣2x+12.
∵点Q(m,3)在直线A′B上,
∴3=﹣2m+12
解得:m=![]() ,
,
故存在m的值使得QA+QB最小,此时点Q的坐标为(![]() ,3).
,3).


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y1=ax+b(a≠0)的图象与反比例函数y2=![]() (k≠0)的图象交于A、B两点,与x轴交于点C,过点A作AH⊥x轴于点H,点O是线段CH的中点,AC=4
(k≠0)的图象交于A、B两点,与x轴交于点C,过点A作AH⊥x轴于点H,点O是线段CH的中点,AC=4![]() ,cos∠ACH=
,cos∠ACH=![]() .
.
(1)求该反比例函数和一次函数的解析式;
(2)在x轴上是否存在点P,使三角形PAC是等腰三角形?若存在,请求出P点坐标;不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算或化简:
(1)3-(-8)+(-5)+6
(2)![]() .
.
(3)-23×(-8)-(-![]() )3×(-16)+
)3×(-16)+![]() ×(-3)2
×(-3)2
(4)先化简,再求值:
![]() ,其中
,其中![]() ,
,![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)下列关于反比例函数y=![]() 的性质,描述正确的有_____。(填所有描述正确的选项)
的性质,描述正确的有_____。(填所有描述正确的选项)
A. y随x的增大而减小
B. 图像关于原点中心对称
C. 图像关于直线y=x成轴对称
D. 把双曲线y=![]() 绕原点逆时针旋转90°可以得到双曲线y=-
绕原点逆时针旋转90°可以得到双曲线y=-![]()
(2)如图,直线AB、CD经过原点且与双曲线y=![]() 分别交于点A、B、C、D,点A、C的横坐标分别为m,n(m>n>0),连接AC、CB、BD、DA。
分别交于点A、B、C、D,点A、C的横坐标分别为m,n(m>n>0),连接AC、CB、BD、DA。
①判断四边形ACBD的形状,并说明理由;
②当m、n满足怎样的数量关系时,四边形ACBD是矩形?请直接写出结论;
③若点A的横坐标m=3,四边形ACBD的面积为S,求S与n之间的函数表达式。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在Rt△ABC中,∠C=90°,AC=9,BC=12,点 D、E 分别在边AC、BC上,且CD:CE=3︰4.将△CDE绕点D顺时针旋转,当点C落在线段DE上的点 F处时,BF恰好是∠ABC的平分线,此时线段CD的长是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两个工程队承包了地铁某标段全长3900米的施工任务,分别从南,北两个方向同时向前掘进。已知甲工程队比乙工程队平均每天多掘进0.4米经过13天的施工两个工程队共掘进了156米.
(1)求甲,乙两个工程队平均每天各掘进多少米?
(2)为加快工程进度两工程队都改进了施工技术,在剩余的工程中,甲工程队平均每天能比原来多掘进0.4米,乙工程队平均每天能比原来多掘进0.6米,按此施工进度能够比原来少用多少天完成任务呢?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个三角形数阵,仔细观察排列规律:
第1行 1
第2行 -![]()
![]()
第3行 -![]()
![]() -
-![]()
第4行 ![]() -
-![]()
![]() -
-![]()
.....
按照这个规律继续排列下去,第21行第2个数是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】河南省旅游资源丰富,2013~2017年旅游收入不断增长,同比增速分别为:15.3%,12.7%,15.3%,14.5%,17.1%.关于这组数据,下列说法正确的是( )
A. 中位数是12.7% B. 众数是15.3%
C. 平均数是15.98% D. 方差是0
查看答案和解析>>
科目:初中数学 来源: 题型:
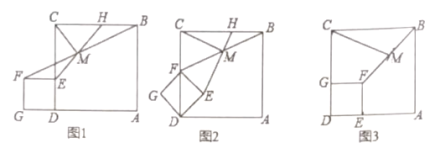
【题目】如图1,点![]() 是正方形
是正方形![]() 边
边![]() 上任意一点,以
上任意一点,以![]() 为边作正方形
为边作正方形![]() ,连接
,连接![]() ,点
,点![]() 是线段
是线段![]() 中点,射线
中点,射线![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() .
.
(1)请直接写出![]() 和
和![]() 的数量关系和位置关系.
的数量关系和位置关系.
(2)把图1中的正方形![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,此时点
,此时点![]() 恰好落在线段
恰好落在线段![]() 上,如图2,其他条件不变,(1)中的结论是否成立,请说明理由.
上,如图2,其他条件不变,(1)中的结论是否成立,请说明理由.
(3)把图1中的正方形![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,此时点
,此时点![]() 、
、![]() 恰好分别落在线段
恰好分别落在线段![]() 、
、![]() 上,连接
上,连接![]() ,如图3,其他条件不变,若
,如图3,其他条件不变,若![]() ,
,![]() ,直接写出
,直接写出![]() 的长度.
的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com