
【题目】如图,在平面直角坐标系中,一次函数y1=ax+b(a≠0)的图象与反比例函数y2=![]() (k≠0)的图象交于A、B两点,与x轴交于点C,过点A作AH⊥x轴于点H,点O是线段CH的中点,AC=4
(k≠0)的图象交于A、B两点,与x轴交于点C,过点A作AH⊥x轴于点H,点O是线段CH的中点,AC=4![]() ,cos∠ACH=
,cos∠ACH=![]() .
.
(1)求该反比例函数和一次函数的解析式;
(2)在x轴上是否存在点P,使三角形PAC是等腰三角形?若存在,请求出P点坐标;不存在,请说明理由.

【答案】(1)反比例函数的解析式为:y2=﹣![]() ,一次函数解析式为y1=﹣2x+4;(2)P点坐标为(﹣8,0).
,一次函数解析式为y1=﹣2x+4;(2)P点坐标为(﹣8,0).
【解析】分析:(1)解直角△ACH求得CH与AH,即可得点A的坐标;由点A,C的坐标,用待定系数法求直线AB的解析式;(2)因为点A,C确定,点P在x轴上,所以设P(m,0),分三种情况求解,①顶点是点A时,②顶点是点C时,③顶点是点P时.
详解:(1)∵AC=![]() ,cos∠ACH=
,cos∠ACH=![]() ,∴
,∴![]() ,
,
解得CH=4,
由勾股定理得,AH=![]() =8,
=8,
∵点O是线段CH的中点,
∴点A的坐标为(﹣2,8),点C的坐标为(2,0),
∴反比例函数的解析式为:y2=﹣![]() ,
,
由点A,C的坐标列方程组![]() ,
,
解得,![]() ,
,
∴一次函数解析式为y1=﹣2x+4;
(2)设P点坐标为(m,0),
①当点A为等腰三角形的顶点时,PH=CH=4,则OP=6,
∴P点坐标为(﹣6,0);
②当点C为等腰三角形的顶点时,PC=CA=![]() ,
,
则OP=![]() +2或
+2或![]() ﹣2,
﹣2,
∴P点坐标为(2﹣![]() ,0)或(
,0)或(![]() +2,0);
+2,0);
③当点P为顶点时,点P为AC垂直平分线与x轴的交点,PA=PC,
则(2﹣m)2=(﹣2﹣m)2+82,
解得,m=﹣8,
∴P点坐标为(﹣8,0).,


 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】如图,OM是∠AOC的平分线.ON是∠BOC的平分线.
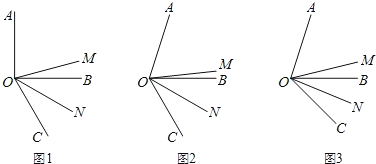
(1)如图1,当∠AOB=90°,∠BOC=60°时,∠MON的度数是多少?为什么?
(2)如图2,当∠AOB=70°,∠BOC=60°时,∠MON= (直接写出结果)
(3)如图3,当∠AOB=α,∠BOC=β时,猜想:∠MON﹣∠CON= (直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A的坐标为(﹣![]() ,0),点B的坐标为(0,3).
,0),点B的坐标为(0,3).
(1)求过A,B两点直线的函数表达式;
(2)过B点作直线BP与x轴交于点P,且使OP=2OA,求△ABP的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】重庆市江津区是中国著名的“花椒之乡”,其地理气候条件优越,所产花椒麻香味浓, 并且富含多种微量元素,出油率高,不仅是优良的调味品,而且经加工,可提取多种名贵的化工原料.去年江津某村积极改革农村产业结构,增加农名收入,村委会多方筹集资金,流转耕地 1200 亩,全都用于种植大红袍花椒和九叶青花椒两个品种,花椒上市后,大红袍花椒每
亩获利 1000 元,九叶青花椒每亩获利 1200 元.
(1)去年该村种植的1200亩花椒,至少获利128万元,则该村种植大红花胶的面积最多为多少亩?
(2)今年村里保持(1)中大红袍花椒的最多面积种植大红袍花椒,且每亩的获利比去年增加![]() a%;由于九叶青花椒每亩获利较多,村里利用新增流转耕地,使九叶青花椒的种植面积,在去年最少种植面积的基础上扩大2a%,同时每亩利润将增加
a%;由于九叶青花椒每亩获利较多,村里利用新增流转耕地,使九叶青花椒的种植面积,在去年最少种植面积的基础上扩大2a%,同时每亩利润将增加![]() a%,这样今年花椒的总利润达到了208万元,求a的值.
a%,这样今年花椒的总利润达到了208万元,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知:点A和点B(如图1),根据条件画图(用三角板和量角器):
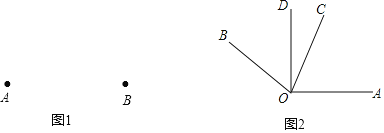
①画射线BA;
②画∠ABC=90°,使得点C在线段AB上方且AB=BC;
③连接AC,画出∠ABC的角平分线BD,交AC于D.通过观察、度量、猜想获得线段BD、AC的关系.
(2)已知:如图2,∠AOB=150,OC平分∠AOB,AO⊥DO,求∠COD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在正方形ABCD中,E为CD边上的一点,F为BC的延长线上一点,CE=CF。
⑴△BCE与△DCF全等吗?说明理由;
⑵若∠BEC=60o,求∠EFD。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将口ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.
(1)求证:△ABF≌△ECF
(2)若∠AFC=2∠D,连接AC、BE.求证:四边形ABEC是矩形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过点A(0,3)的一次函数y1=kx+b(k≠0)的图象与正比例函数y2=2x的图象相交于点B,且点B的横坐标是1.
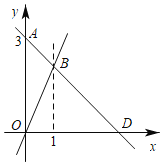
(1)求点B的坐标及k、b的值;
(2)若该一次函数的图象与x轴交于D点,求△BOD的面积
(3)当y1≤y2时,自变量x的取值范围为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
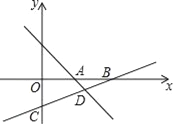
【题目】如图,直线l1:y=﹣x+3与x轴相交于点A,直线l2:y=kx+b经过点(3,﹣1),与x轴交于点B(6,0),与y轴交于点C,与直线l1相交于点D.
(1)求直线l2的函数关系式;
(2)点P是l2上的一点,若△ABP的面积等于△ABD的面积的2倍,求点P的坐标;
(3)设点Q的坐标为(m,3),是否存在m的值使得QA+QB最小?若存在,请求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com