
【题目】如图,过点A(0,3)的一次函数y1=kx+b(k≠0)的图象与正比例函数y2=2x的图象相交于点B,且点B的横坐标是1.
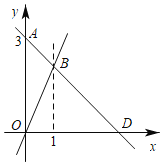
(1)求点B的坐标及k、b的值;
(2)若该一次函数的图象与x轴交于D点,求△BOD的面积
(3)当y1≤y2时,自变量x的取值范围为 .
【答案】(1)B(1,2),![]() ,
,![]() ;(2)△BOD的面积3;(3)x≥1.
;(2)△BOD的面积3;(3)x≥1.
【解析】
(1)先利用正比例函数解析式确定B点坐标,然后利用待定系数法求一次函数解析式,从而得到k、b的值;
(2)先确定D点坐标,然后利用三角形面积公式计算△BOD的面积;
(3)结合函数图象,写出自变量x的取值范围.
(1)当x=1时,y2=2x=2,则B(1,2),
把A(0,3),B(1,2)代入y=kx+b得
![]() ,解得
,解得![]() ,
,
所以一次函数解析式为y=-x+3;
(2)当x=0时,-x+3=0,解得x=3,则D(3,0),
所以△BOD的面积=![]() ×3×2=3;
×3×2=3;
(3)当y1≤y2时,自变量x的取值范围为x≥1.
故答案为x≥1.


科目:初中数学 来源: 题型:
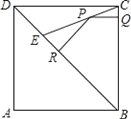
【题目】如图,E是边长为1的正方形ABCD的对角线BD上的一点,且BE=BA,P是CE上任意一点,PQ⊥BC于点Q,PR⊥BE于点R.则:(1)DE=__;(2)PQ+PR=__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y1=ax+b(a≠0)的图象与反比例函数y2=![]() (k≠0)的图象交于A、B两点,与x轴交于点C,过点A作AH⊥x轴于点H,点O是线段CH的中点,AC=4
(k≠0)的图象交于A、B两点,与x轴交于点C,过点A作AH⊥x轴于点H,点O是线段CH的中点,AC=4![]() ,cos∠ACH=
,cos∠ACH=![]() .
.
(1)求该反比例函数和一次函数的解析式;
(2)在x轴上是否存在点P,使三角形PAC是等腰三角形?若存在,请求出P点坐标;不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小苏和小林在如图所示的跑道上进行4×50米折返跑.在整个过程中,跑步者距起跑线的距离y(单位:m)与跑步时间t(单位:s)的对应关系如下图所示.下列叙述正确的是( )

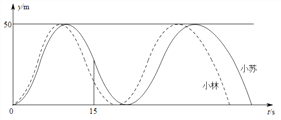
A. 两人从起跑线同时出发,同时到达终点
B. 小苏跑全程的平均速度大于小林跑全程的平均速度
C. 小苏前15s跑过的路程大于小林前15s跑过的路程
D. 小林在跑最后100m的过程中,与小苏相遇2次
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,DB∥AC,且DB=![]() AC,E是AC的中点.
AC,E是AC的中点.

(1)求证:四边形BDEC是平行四边形;
(2)连接AD、BE,△ABC添加一个条件: ,使四边形DBEA是矩形(不需说明理由).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校学生利用双休时间去距学校10 km的天平山社会实践活动,一部分学生骑电瓶车先走,过了20 min后,其余学生乘公交车沿相同路线出发,结果他们同时到达.已知公交车的速度是电瓶车学生速度的2倍,求骑电瓶车学生的速度和公交车的速度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算或化简:
(1)3-(-8)+(-5)+6
(2)![]() .
.
(3)-23×(-8)-(-![]() )3×(-16)+
)3×(-16)+![]() ×(-3)2
×(-3)2
(4)先化简,再求值:
![]() ,其中
,其中![]() ,
,![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)下列关于反比例函数y=![]() 的性质,描述正确的有_____。(填所有描述正确的选项)
的性质,描述正确的有_____。(填所有描述正确的选项)
A. y随x的增大而减小
B. 图像关于原点中心对称
C. 图像关于直线y=x成轴对称
D. 把双曲线y=![]() 绕原点逆时针旋转90°可以得到双曲线y=-
绕原点逆时针旋转90°可以得到双曲线y=-![]()
(2)如图,直线AB、CD经过原点且与双曲线y=![]() 分别交于点A、B、C、D,点A、C的横坐标分别为m,n(m>n>0),连接AC、CB、BD、DA。
分别交于点A、B、C、D,点A、C的横坐标分别为m,n(m>n>0),连接AC、CB、BD、DA。
①判断四边形ACBD的形状,并说明理由;
②当m、n满足怎样的数量关系时,四边形ACBD是矩形?请直接写出结论;
③若点A的横坐标m=3,四边形ACBD的面积为S,求S与n之间的函数表达式。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】河南省旅游资源丰富,2013~2017年旅游收入不断增长,同比增速分别为:15.3%,12.7%,15.3%,14.5%,17.1%.关于这组数据,下列说法正确的是( )
A. 中位数是12.7% B. 众数是15.3%
C. 平均数是15.98% D. 方差是0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com