
����Ŀ����ͼ1����![]() ��������
��������![]() ��
��![]() ������һ�㣬��
������һ�㣬��![]() Ϊ����������
����������![]() ������
������![]() ����
����![]() ���߶�
���߶�![]() �е㣬����
�е㣬����![]() ��
��![]() ���ڵ�
���ڵ�![]() ������
������![]() ��
��
��1����ֱ��д��![]() ��
��![]() ��������ϵ��λ�ù�ϵ��
��������ϵ��λ�ù�ϵ��
��2����ͼ1�е�������![]() �Ƶ�
�Ƶ�![]() ˳ʱ����ת
˳ʱ����ת![]() ����ʱ��
����ʱ��![]() ǡ�������߶�
ǡ�������߶�![]() �ϣ���ͼ2�������������䣬��1���еĽ����Ƿ��������˵�����ɣ�
�ϣ���ͼ2�������������䣬��1���еĽ����Ƿ��������˵�����ɣ�
��3����ͼ1�е�������![]() �Ƶ�
�Ƶ�![]() ˳ʱ����ת
˳ʱ����ת![]() ����ʱ��
����ʱ��![]() ��
��![]() ǡ�÷ֱ������߶�
ǡ�÷ֱ������߶�![]() ��
��![]() �ϣ�����
�ϣ�����![]() ����ͼ3�������������䣬��
����ͼ3�������������䣬��![]() ��
��![]() ��ֱ��д��
��ֱ��д��![]() �ij��ȣ�
�ij��ȣ�
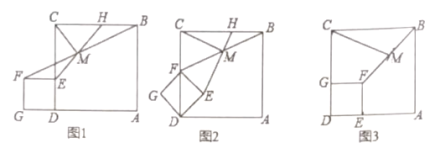
���𰸡���1��![]() ����2������������3��
����2������������3��![]() .
.
��������
(1)֤����FME����AMH���õ�HM=EM�����ݵ���ֱ�������ε����ʿɵý���. ��2�����������ε����ʵõ���A��E��C��ͬһ��ֱ����,����ֱ��������б���ϵ����ߵ���б�ߵ�һ���֪. ��3����ͼ3�У�����EC��EM���ɣ�1����2����֪����CME�ǵ���ֱ�������Σ����õ���ֱ�������ε����ʽ�����⼴�ɣ�
�⣺��1�����ۣ�CM��ME��CM��EM��
���ɣ���AD��EF��AD��BC��
��BC��EF��
���EFM����HBM��
����FME����BMH��
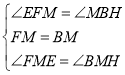
���FME�ա�BMH��ASA����
��HM��EM��EF��BH��
��CD��BC��
��CE��CH���ߡ�HCE��90����HM��EM��
��CM��ME��CM��EM��
��2����ͼ2������![]() ��
��
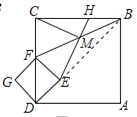
���ı���![]() ���ı���
���ı���![]() �������Σ�
��������
��![]()
���![]() ��ͬһ��ֱ���ϣ�
��ͬһ��ֱ���ϣ�
��![]() ��
��![]() Ϊ
Ϊ![]() ���е㣬
���е㣬
��![]() ��
��![]() ����
����![]() ��
��
��![]() ����
����![]() ��
��
��![]() ��
��
��![]()
��![]() ��
��
��![]() ��
��
��![]() ��
��
��3����ͼ3�У�����EC��EM��
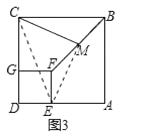
�ɣ�1����2����֪����CME�ǵ���ֱ�������Σ�
��![]()
��CM��EM��![]()



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
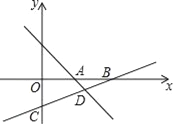
����Ŀ����ͼ��ֱ��l1��y=��x+3��x���ཻ�ڵ�A��ֱ��l2��y=kx+b�����㣨3����1������x�ύ�ڵ�B��6��0������y�ύ�ڵ�C����ֱ��l1�ཻ�ڵ�D��
��1����ֱ��l2�ĺ�����ϵʽ��
��2����P��l2�ϵ�һ�㣬����ABP�����������ABD�������2�������P�����ꣻ
��3�����Q������Ϊ��m��3�����Ƿ����m��ֵʹ��QA+QB��С�������ڣ��������Q�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O��ֱ��AB=8��CΪ��AB���е㣬PΪ��O��һ���㣬����AP��CP����C��CD��CP��AP�ڵ�D����P��B�˶���Cʱ�����D�˶���·����Ϊ____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ţ�1������֯�༶�����ᣬ������齱���ڣ�ÿ��ͬѧ����һ�γ齱���ᣬ�齱�������£���һ���˿����е���Ϊ��2������3������3������5������6���������Ʊ��泯��ϴ�ȣ��ȴ��г��1���ƣ��ٴ����µ�4�����г��1���ƣ���¼�����Ƶ�����Żأ����һ�γ齱����ÿ�γ�������Ƶ���֮��Ϊ![]() ��������Ҫ��ȷ�����
��������Ҫ��ȷ�����

��1�����б�����״ͼ�ķ��������ͬѧ���һ�Ƚ��ĸ��ʣ�
��2���Ƿ�ÿ�γ齱�����Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��l1�Ľ���ʽΪy=��x+2��l1��x�ύ�ڵ�B��ֱ��l2������D��0��5������ֱ��l1���ڵ�C����1��m��������x�ύ�ڵ�A,
��1�����C�����꼰ֱ��l2�Ľ���ʽ��
��2������ABC�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������һ�ֿ�ʳ�õ�Ұ����������ʱ������������г��۸�30Ԫ/ǧ���չ�������Ұ����1000ǧ�˴��������У���Ԥ�⣬��Ұ�������г��۸���ÿ��ÿǧ������1Ԫ�����䶳�������Ұ����ʱÿ����Ҫ֧�����ַ��úϼ�307Ԫ����������Ұ�������������ౣ��160�죬ͬʱ��ƽ��ÿ����3ǧ�˵�Ұ�������ܳ��ۣ�
��1�������x�������Ұ����һ���Գ��ۣ�������Ұ�����������ܶ�ΪPԪ����д��P��x֮��ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
��2�����������Ұ�����Ŷ��������ۿɻ���������WԪ��������=�����ܶ�չ��ɱ������ַ��ã�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�E��AD�е㣬����ABE��ֱ��BE�۵���õ���GBE���ӳ�BG��CD��F����AB=6��BC=![]() ����CF�ij�Ϊ_______
����CF�ij�Ϊ_______

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�һ�κ���y=��2x+8��ͼ����x�ᣬy��ֱ��ڵ�A����C������A��AB��x�ᣬ����Ϊ��A������C��CB��y�ᣬ����Ϊ��C�����������ཻ�ڵ�B��

��1���߶�AB��BC��AC�ij��ֱ�ΪAB=�� ����BC=�� ����AC=�� ����
��2���۵�ͼ1�е���ABC��ʹ��A���C�غϣ��ٽ��۵����ͼ��չ�����ۺ�DE��AB�ڵ�D����AC�ڵ�E������CD����ͼ2��
�������A��B��������ѡһ��������ѡ���� ���⣮
A�������߶�AD�ij���
����y���ϣ��Ƿ���ڵ�P��ʹ����APDΪ���������Σ������ڣ���ֱ��д���������������е�P�����ꣻ�������ڣ���˵�����ɣ�
B�������߶�DE�ij���
��������ƽ���ڣ��Ƿ���ڵ�P������B�⣩��ʹ���Ե�A��P��CΪ���������������ABCȫ�ȣ������ڣ���ֱ��д�����з��������ĵ�P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C=90�㣬��ACD��AD�۵���ʹ�õ�C����б��AB�ϵĵ�E����
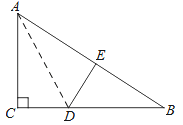
��1����֤����BDE�ס�BAC��
��2����֪AC=6��BC=8�����߶�AD�ij��ȣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com