
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�һ�κ���y=��2x+8��ͼ����x�ᣬy��ֱ��ڵ�A����C������A��AB��x�ᣬ����Ϊ��A������C��CB��y�ᣬ����Ϊ��C�����������ཻ�ڵ�B��

��1���߶�AB��BC��AC�ij��ֱ�ΪAB=�� ����BC=�� ����AC=�� ����
��2���۵�ͼ1�е���ABC��ʹ��A���C�غϣ��ٽ��۵����ͼ��չ�����ۺ�DE��AB�ڵ�D����AC�ڵ�E������CD����ͼ2��
�������A��B��������ѡһ��������ѡ���� ���⣮
A�������߶�AD�ij���
����y���ϣ��Ƿ���ڵ�P��ʹ����APDΪ���������Σ������ڣ���ֱ��д���������������е�P�����ꣻ�������ڣ���˵�����ɣ�
B�������߶�DE�ij���
��������ƽ���ڣ��Ƿ���ڵ�P������B�⣩��ʹ���Ե�A��P��CΪ���������������ABCȫ�ȣ������ڣ���ֱ��д�����з��������ĵ�P�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��8��4��4![]() ����2��������.
����2��������.
�������������������1����ȷ����OA=4��OC=8�������ó�AB=8��BC=4�����ù��ɶ������ɵó�AC��
��2��A���������۵������ʵó�BD=8��AD������ù��ɶ������ɵó�������
�ڷ�����������÷��̵�˼�뼴�ɵó�������
B���������۵������ʵó�AE�����ù��ɶ������ɵó�������
�����жϳ���APC=90�㣬�ٷ�������ۼ��㼴�ɣ�
���������������1����һ�κ���y=��2x+8��ͼ����x����y��ֱ��ڵ�A����C����A��4��0����C��0��8������OA=4��OC=8����AB��x����CB��y������AOC=90�㣬���ı���OABC�Ǿ�������AB=OC=8��BC=OA=4����Rt��ABC�������ݹ��ɶ�������AC=![]() =4
=4![]() ���ʴ�Ϊ��8��4��4
���ʴ�Ϊ��8��4��4![]() ��
��
��2��ѡA�����ɣ�1��֪��BC=4��AB=8�����۵�֪��CD=AD����Rt��BCD����BD=AB��AD=8��AD�����ݹ��ɶ�������CD2=BC2+BD2������AD2=16+��8��AD��2����AD=5��
���ɢ�֪��D��4��5������P��0��y������A��4��0������AP2=16+y2��DP2=16+��y��5��2���ߡ�APDΪ�������������������������ۣ�
����AP=AD����16+y2=25����y=��3����P��0��3����0����3����
����AP=DP����16+y2=16+��y��5��2����y=![]() ����P��0��
����P��0��![]() ����
����
����AD=DP��25=16+��y��5��2����y=2��8����P��0��2����0��8����
����������P��0��3����0����3����P��0��![]() ����P��0��2����0��8����
����P��0��2����0��8����
ѡB������A��֪��AD=5�����۵�֪��AE=![]() AC=2
AC=2![]() ��DE��AC��E����Rt��ADE����DE=
��DE��AC��E����Rt��ADE����DE=![]() =
=![]() ��
��
�ڡ��Ե�A��P��CΪ��������������ABCȫ�������APC�ա�ABC�����CPA�ա�ABC�����APC=��ABC=90�㣮���ı���OABC�Ǿ��������ACO�ա�CAB����ʱ��������������P�͵�O�غ�������P��0��0����
��ͼ3������O��ON��AC��N����֤����AON�ס�ACO����![]() ����
����![]() ����AN=
����AN=![]() ������N��NH��OA����NH��OA�����ANH�ס�ACO����
������N��NH��OA����NH��OA�����ANH�ס�ACO����![]() ����
����![]() ����NH=
����NH=![]() ��AH=
��AH=![]() ����OH=
����OH=![]() ����N��
����N��![]() ��������P2���O����AC�Գ�����P2��
��������P2���O����AC�Գ�����P2��![]() ����ͬ������B����AC�ĶԳƵ�P1��ͬ�ϵķ�������P1����
����ͬ������B����AC�ĶԳƵ�P1��ͬ�ϵķ�������P1����![]() ����
����
�������������������ĵ�P������Ϊ����0��0������![]() ��������
��������![]() ����
����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������ϱ�������е��У��������������ľ�����ȣ���֪��A��ʾ��12����G��ʾ6��
![]()
��1����ʾԭ��ĵ�������������C��ʾ����������������
��2��������������M��N����M����D�ľ���Ϊ![]() ����N����D�ľ���Ϊ4�����M��N֮��ľ��룻
����N����D�ľ���Ϊ4�����M��N֮��ľ��룻
��3����PΪ������һ�㣬�ұ�ʾ��������������P����A�ľ������P����G�ľ���֮��Ϊ18���������ĵ�P��������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��y=��3x+3��x�ᡢy��ֱ���A��B���㣬��ABΪ���ڵ�һ������������ABCD��x�Ḻ����ƽ��a����λ���Ⱥ�Cǡ������˫�����ϣ���a��ֵ�� ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ʽ��2x2+ax��y+6������2bx2��3x+5y��1����ֵ����ĸx��ȡ��ֵ�أ�����ʽ![]() a2��2b2����
a2��2b2����![]() a3��3b2����_____
a3��3b2����_____
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�ӹ�A�����60������ʱ����Ҽӹ�B�����80������ʱ����ͬ���ס�������ÿ�칲�ӹ�35����������ÿ��ӹ�x��A�������
��1��ֱ��д����ÿ��ӹ���������������ú�x�Ĵ���ʽ��ʾ��
��2����ס���ÿ����ӹ�������ٸ���
��3�������г�Ԥ�⣬�ӹ�A���������õ�����ΪmԪ/����3��m��5�����ӹ�B���������õ�����ÿ����A����1Ԫ����ס���ÿ��ӹ����������õ�������P��Ԫ����m�ĺ�����ϵʽ������P�����ֵ����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C=90������ACΪֱ������O����AB��D������O��OE��AB����BC��E��
��1����֤��EDΪ��O�����ߣ�
��2�������O�İ뾶Ϊ![]() ��ED=2���ӳ�EO����O��F������DF��AF������ADF�������
��ED=2���ӳ�EO����O��F������DF��AF������ADF�������

���𰸡���1��֤������������2��![]()
�������������������1����������OD����OE��AB������ƽ��������������ε����ʣ���֤��![]() ��
��![]() ���ɵ�
���ɵ�![]() �����֤��
�����֤��![]() Ϊ
Ϊ![]() �����ߣ�
�����ߣ�
��2������CD������ֱ�����Ե�Բ�ܽ���ֱ�ǣ����ɵ�![]() ���ù��ɶ����������
���ù��ɶ����������![]() �ij�������OE��AB��֤��
�ij�������OE��AB��֤��![]() �������������εĶ�Ӧ�߳ɱ������������
�������������εĶ�Ӧ�߳ɱ������������![]() �ij���Ȼ���������Ǻ�����֪ʶ�����
�ij���Ȼ���������Ǻ�����֪ʶ�����![]() ��
��![]() �ij���Ȼ������S��ADF=S����ABEF-S����DBEF��ô𰸣�
�ij���Ȼ������S��ADF=S����ABEF-S����DBEF��ô𰸣�
���������(1)֤��������OD��

��OE��AB��
���COE=��CAD����EOD=��ODA��
��OA=OD,
���OAD=��ODA��
���COE=��DOE��
�ڡ�COE�͡�DOE�У�
 ���COE�ա�DOE(SAS)��
���COE�ա�DOE(SAS)��
![]()
��ED��OD��
��ED��![]() �����ߣ�
�����ߣ�
(2)����CD����OE��M��
��Rt��ODE��
��OD=32��DE=2��
![]()
��OE��AB��
���COE�ס�CAB��
![]() ��AB=5��
��AB=5��
��AC��ֱ����
![]()
![]()
![]()
![]()
��EF��AB��
![]()
![]()
![]()
��S��ADF=S����ABEFS����DBEF
![]()
���ADF�����Ϊ![]()

�����͡������
��������
25
����Ŀ������Ŀ����֪��������y=ax2+ax+b��a��0����ֱ��y=2x+m��һ��������M��1��0������a��b��
��1����b��a�Ĺ�ϵʽ�������ߵĶ���D���꣨��a�Ĵ���ʽ��ʾ����
��2��ֱ���������ߵ�����һ�������ΪN������DMN�������a�Ĺ�ϵʽ��
��3��a=��1ʱ��ֱ��y=��2x���������ڵڶ������ڵ�G����G��H����ԭ��Գƣ��ֽ��߶�GH��y������ƽ��t����λ��t��0�������߶�GH����������������ͬ�Ĺ����㣬����t��ȡֵ��Χ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲����е�ʽ����������⣺
��![]() ��
��
��![]() ��
��
��![]() ������
������
��1��![]() .
.
��2�����ù�ʽ��![]() �Ľ����
�Ľ����
��3��С��ϲ���Ķ�������������Ȿ�飬���ҳ����������������1��2��3��4������9��10����һ�������Ѿ�������ҳ�밴��˳�����ʱ����С�İ�����һ��ҳ��������Σ������ǡ�õ���2018����������ε�ҳ���ǵ� ҳ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾���з�һ�ְ칫���ñڹ�ʽ����������װ���һ�鳤���δſ飬����31öԲ����С��Ƭ�������������ڵװ�����Ϊ���ڣ���ͼ1��2007��10�·�����
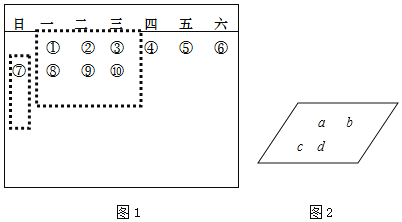
��1���ó����κ������ηֱ�Ȧ�����ڵ�3������9����������Ȧ��������������Ϊa���ú�a����ʽ��ʾ��3�����ĺ���9�����ĺͣ�����ֱ�Ϊ�� ������ ����
��2����ij��ͼ��Ȧ�����ڵ�5������ʹ��5�����ĺ��ܱ�ʾ��5a����ʽ������ͼ2�л���һ��������ͼ�Σ�
��3����ƽ���ı���Ȧ�����ڵ��ĸ������Ƿ����������4����ʹ��a+b+c+d��114��������ھ��������������˵�����ɣ�
��4����һ�η���31ö������Ƭ���ڶ��η������е�30ö�������η������е�29ö����������31��ֻ�������е�һö���������ķ�������������Ƭ���ܷ�ʹ���������е�31ö��Ƭԭ�������ֵ�һ�涼���£���ͨ������֤������жϣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����˾��С�����������Ӫ��ȫ���ڶ���������������Ͻ��еģ�����涨��Ϊ��������Ϊ���������������г�������£�+15,-2,+3,-1,+10,-3,-2.
(1)�����һ���˿�����Ŀ�ĵ�ʱ��С������������ʱ�ij������Զ��
(2)������������Ϊ![]() ����������С����Ͷ���L��
����������С����Ͷ���L��
(3)С�������ij������۲��Ź涨����(������3km)5Ԫ������3km�����IJ���ÿǧ���շ�1Ԫ��С�����������������Ԫ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com