
【题目】某公司新研发一种办公室用壁挂式电磁日历,底板是一块长方形磁块,再用31枚圆柱形小铁片标上数字吸附在底板上作为日期,如图1是2007年10月份日历
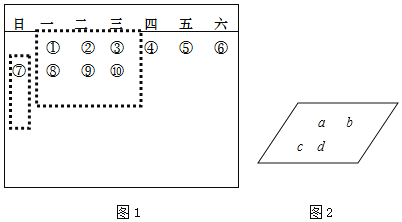
(1)用长方形和正方形分别圈出相邻的3个数和9个数,若设圈出的数的中心数为a,用含a的整式表示这3个数的和与9个数的和,结果分别为 , .
(2)用某种图形圈出相邻的5个数,使这5个数的和能表示成5a的形式,请在图2中画出一个这样的图形.
(3)用平行四边形圈出相邻的四个数,是否存在这样的4个数使得a+b+c+d=114?如果存在就求出来,不存在说明理由.
(4)第一次翻动31枚日历铁片,第二次翻动其中的30枚,第三次翻动其中的29枚,……,第31次只翻动其中的一枚,按这样的方法翻动日历铁片,能否使铁板上所有的31枚铁片原来有数字的一面都朝下,试通过计算证明你的判断.
【答案】(1)3a,9a;(2)见解析;(3)不存在,理由见解析;(4)不能,证明见解析
【解析】
(1)根据日历的特点可列出关于a的方程,求解即可;
(2)根据上下左右的数量关系,画图即可;
(3)举例拆分即可.
(4)根据数字的奇偶性规律验证.
(1)长方形中中间数为a,上下两数分别为(a﹣7);(a+7)
∴3个数的和为a+(a﹣7)+(a+7)=3a
正方形中中间数为a,那么左右两数分别为(a﹣1);(a+1)
根据以上规律左边三个数的和为3(a﹣1);中间三个数的和为3a;右边三个数的和为3(a+1)
∴9个数的和为3(a﹣1)+3a+3(a+1)=9a
故答案为:3a,9a.
(2)如图所示即可
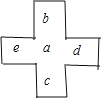
(3)不存在,
根据图形的规律得,b=a+1,c=a+6,d=a+7,
∵a+b+c+d=114,
∴a+a+1+a+6+a+7=114,
a=25,
∴d=a+25=32,
∴不存在这样的4个数使得a+b+c+d=114.
(4)不能,
共翻动了![]() (次),
(次),
而要使一个铁皮翻面,需要奇数次,
所有的31枚铁片原来有数字的一面都朝下需要31 ![]() 奇数次,
奇数次,
∵496不是奇数,
∴第一次翻动31枚日历铁片,第二次翻动其中的30枚,第三次翻动其中的29枚,……,第31次只翻动其中的一枚,按这样的方法翻动日历铁片,不能使铁板上所有的31枚铁片原来有数字的一面都朝下.


科目:初中数学 来源: 题型:
【题目】问题提出
![]() 如图1,点A为线段BC外一动点,且
如图1,点A为线段BC外一动点,且![]() ,填空:当点A位于______时,线段AC的长取得最大值,且最大值为______
,填空:当点A位于______时,线段AC的长取得最大值,且最大值为______![]() 用含
用含![]() 的式子表示
的式子表示![]() .
.
问题探究
![]() 点A为线段BC外一动点,且
点A为线段BC外一动点,且![]() ,如图2所示,分别以
,如图2所示,分别以![]() 为边,作等边三角形ABD和等边三角形ACE,连接
为边,作等边三角形ABD和等边三角形ACE,连接![]() ,找出图中与BE相等的线段,请说明理由,并直接写出线段BE长的最大值.
,找出图中与BE相等的线段,请说明理由,并直接写出线段BE长的最大值.
问题解决:
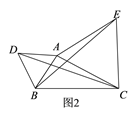
![]() 如图3,在平面直角坐标系中,点A的坐标为
如图3,在平面直角坐标系中,点A的坐标为![]() ,点B的坐标为
,点B的坐标为![]() ,点P为线段AB外一动点,且
,点P为线段AB外一动点,且![]() ,求线段AM长的最大值及此时点P的坐标.
,求线段AM长的最大值及此时点P的坐标.
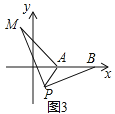
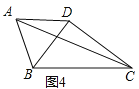
![]() 如图4,在四边形ABCD中,
如图4,在四边形ABCD中, ![]() ,若对角线
,若对角线![]() 于点D,请直接写出对角线AC的最大值.
于点D,请直接写出对角线AC的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,一次函数y=﹣2x+8的图象与x轴,y轴分别交于点A,点C,过点A作AB⊥x轴,垂足为点A,过点C作CB⊥y轴,垂足为点C,两条垂线相交于点B.

(1)线段AB,BC,AC的长分别为AB= ,BC= ,AC= ;
(2)折叠图1中的△ABC,使点A与点C重合,再将折叠后的图形展开,折痕DE交AB于点D,交AC于点E,连接CD,如图2.
请从下列A、B两题中任选一题作答,我选择 题.
A:①求线段AD的长;
②在y轴上,是否存在点P,使得△APD为等腰三角形?若存在,请直接写出符合条件的所有点P的坐标;若不存在,请说明理由.
B:①求线段DE的长;
②在坐标平面内,是否存在点P(除点B外),使得以点A,P,C为顶点的三角形与△ABC全等?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条不完整的数上从左到右有点A,B,C,其中点A到点B的距离为3,点C到点B的距离为7,如图所示,设点A,B,C所对应的数的和是![]() .
.
![]()
(1)若以点B为原点,则点C所对应的数是 ,若以点C的原点,则![]() 的值是 .
的值是 .
(2)若原点O在图中数轴上,且点C到原点的距离为4,求![]() 的值.
的值.
(3)动点P从点A出发,以每秒2个单位长度的速度向终点C移动,动点Q从点B出发,以每秒1个单位长度的速度向终点C移动,![]() 秒后,P,Q两点间距离为2?(请直接写出答案)
秒后,P,Q两点间距离为2?(请直接写出答案)![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A坐标为(6,0),点B在y轴的正半轴上,且![]() =240.
=240.
(1)求点B坐标;
(2)若点P从B出发沿y轴负半轴方向运动,速度每秒2个单位,运动时间t秒,△AOP的面积为S,求S与t的关系式,并直接写出t的取值范围;
(3)在(2)的条件下,若S△AOP:S△ABP=1:3,且S△AOP+S△ABP=S△AOB,在线段AB的垂直平分线上是否存在点Q,使得△AOQ的面积与△BPQ的面积相等?若存在,求出Q点坐标;若不存在,请说明理由。



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)23×(-5)-(-3)÷![]() ;
;
(2)(-3)×![]() +8×(-2
+8×(-2![]() )-11÷(-
)-11÷(-![]() );
);
(3)(-1)2-(-1![]() )×(-24);
)×(-24);
(4)![]() (-2)2-(
(-2)2-(![]() )3+[1+(-
)3+[1+(-![]() )2×(-1
)2×(-1![]() )].
)].
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一天早晨,乐乐以80米/分的速度上学,5分钟后乐乐的爸爸发现他忘了带数学书,爸爸立即骑自行车以280米/分的速度去追乐乐,并且在途中追上了他,请解决以下问题:
(1)爸爸追上乐乐用了多长时间?
(2)爸爸追上乐乐后,乐乐搭爸爸的自行车回到学校,结果提前了10分钟到校,若爸爸搭上乐乐后的骑行速度为240米/分,求乐乐家离学校有多远.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过点M(-3,2)分别作x轴、y轴的垂线与反比例函数y=![]() 的图象交于A,B两点,则四边形MAOB的面积为( )
的图象交于A,B两点,则四边形MAOB的面积为( )

A. 6B. 8C. 10D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新华商场销售某种冰箱,每台进货价为2500元.市场调研表明:当销售价为2900元时,平均每天能售出8台;而当销售价每降低50元时,平均每天就能多售出4台.商场要想使这种冰箱的销售利润平均每天达到5000元,设每台冰箱的定价为x元,则x满足的关系式为( )
A. (x2500)(8+4×![]() )=5000 B. (2900x2500)(8+4×
)=5000 B. (2900x2500)(8+4×![]() )=5000
)=5000
C. (x2500)(8+4×![]() )=5000 D. (2900x)(8+4×
)=5000 D. (2900x)(8+4×![]() )=5000
)=5000
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com