
ЁОЬтФПЁПЮЪЬтЬсГі
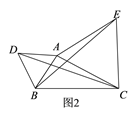
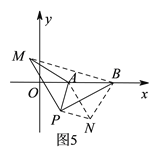
![]() ШчЭМ1ЃЌЕуAЮЊЯпЖЮBCЭтвЛЖЏЕуЃЌЧв
ШчЭМ1ЃЌЕуAЮЊЯпЖЮBCЭтвЛЖЏЕуЃЌЧв![]() ЃЌЬюПеЃКЕБЕуAЮЛгк______ЪБЃЌЯпЖЮACЕФГЄШЁЕУзюДѓжЕЃЌЧвзюДѓжЕЮЊ______
ЃЌЬюПеЃКЕБЕуAЮЛгк______ЪБЃЌЯпЖЮACЕФГЄШЁЕУзюДѓжЕЃЌЧвзюДѓжЕЮЊ______![]() гУКЌ
гУКЌ![]() ЕФЪНзгБэЪО
ЕФЪНзгБэЪО![]() ЃЎ
ЃЎ
ЮЪЬтЬНОП
![]() ЕуAЮЊЯпЖЮBCЭтвЛЖЏЕуЃЌЧв
ЕуAЮЊЯпЖЮBCЭтвЛЖЏЕуЃЌЧв![]() ЃЌШчЭМ2ЫљЪОЃЌЗжБ№вд
ЃЌШчЭМ2ЫљЪОЃЌЗжБ№вд![]() ЮЊБпЃЌзїЕШБпШ§НЧаЮABDКЭЕШБпШ§НЧаЮACEЃЌСЌНг
ЮЊБпЃЌзїЕШБпШ§НЧаЮABDКЭЕШБпШ§НЧаЮACEЃЌСЌНг![]() ЃЌевГіЭМжагыBEЯрЕШЕФЯпЖЮЃЌЧыЫЕУїРэгЩЃЌВЂжБНгаДГіЯпЖЮBEГЄЕФзюДѓжЕЃЎ
ЃЌевГіЭМжагыBEЯрЕШЕФЯпЖЮЃЌЧыЫЕУїРэгЩЃЌВЂжБНгаДГіЯпЖЮBEГЄЕФзюДѓжЕЃЎ
ЮЪЬтНтОіЃК
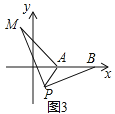
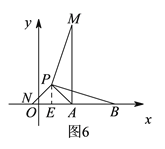
![]() ШчЭМ3ЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЕуAЕФзјБъЮЊ
ШчЭМ3ЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЕуAЕФзјБъЮЊ![]() ЃЌЕуBЕФзјБъЮЊ
ЃЌЕуBЕФзјБъЮЊ![]() ЃЌЕуPЮЊЯпЖЮABЭтвЛЖЏЕуЃЌЧв
ЃЌЕуPЮЊЯпЖЮABЭтвЛЖЏЕуЃЌЧв![]() ЃЌЧѓЯпЖЮAMГЄЕФзюДѓжЕМАДЫЪБЕуPЕФзјБъЃЎ
ЃЌЧѓЯпЖЮAMГЄЕФзюДѓжЕМАДЫЪБЕуPЕФзјБъЃЎ
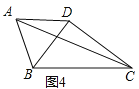
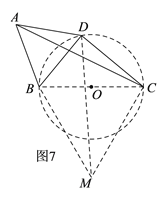
![]() ШчЭМ4ЃЌдкЫФБпаЮABCDжаЃЌ
ШчЭМ4ЃЌдкЫФБпаЮABCDжаЃЌ ![]() ЃЌШєЖдНЧЯп
ЃЌШєЖдНЧЯп![]() гкЕуDЃЌЧыжБНгаДГіЖдНЧЯпACЕФзюДѓжЕЃЎ
гкЕуDЃЌЧыжБНгаДГіЖдНЧЯпACЕФзюДѓжЕЃЎ

ЁОД№АИЁП CBЕФбгГЄЯпЩЯЃЛ ![]()
ЁОНтЮіЁПЗжЮіЃК
ЃЈ1ЃЉгЩЬтвтПЩжЊЃЌЕБЕуAдкCBЕФбгГЄЯпЩЯЪБЃЌЯпЖЮACЕФжЕзюДѓЃЌзюДѓжЕЮЊЃКAC=AB+BC=a+bЃЛ
ЃЈ2ЃЉгЩвбжЊЬѕМўвзжЄЁїABEЁеЁїADCЃЌгЩДЫПЩЕУBE=DCЃЌНсКЯЃЈ1ЃЉжаНсТлПЩжЊЃЌЕБЕуDдкCBЕФбгГЄЯпЩЯЪБЃЌBEзюГЄ=CDзюГЄ=BC+AB=9ЃЛ
ЃЈ3ЃЉЂйШчЯТЭМ5ЃЌСЌНгBMЃЌНЋЁїAPMШЦзХЕуPЫГЪБеыа§зЊ![]() ЕУЕНЁїPBNЃЌСЌНгANЃЌдђЁїAPNЪЧЕШбќжБНЧШ§НЧаЮЃЌдђгЩвбжЊвзЕУAB=3ЃЌAN=
ЕУЕНЁїPBNЃЌСЌНгANЃЌдђЁїAPNЪЧЕШбќжБНЧШ§НЧаЮЃЌдђгЩвбжЊвзЕУAB=3ЃЌAN=![]() AP=
AP=![]() ЃЌНсКЯЃЈ1ЃЉПЩжЊЃЌЕБЕуNдкBAЕФбгГЄЯпЩЯЪБЃЌAMзюДѓ=BNзюДѓ=AB+AN=
ЃЌНсКЯЃЈ1ЃЉПЩжЊЃЌЕБЕуNдкBAЕФбгГЄЯпЩЯЪБЃЌAMзюДѓ=BNзюДѓ=AB+AN=![]() ЃЛШчЭМ6ЃЌЕБЕуNдкBAЕФбгГЄЯпЩЯЪБЃЌЙ§ЕуPзїPEЁЭANгкЕуEЃЌгЩЁїAPNЪЧЕШбќжБНЧШ§НЧаЮЃЌAP=2ЃЌМДПЩЧѓЕУOEКЭPEЕФГЄЃЌДгЖјПЩЕУДЫЪБЕуPЕФзјБъЃЛЂкШчЯТЭМ7ЃЌвдBCЮЊБпзїЕШБпШ§НЧаЮЁїBCMЃЌСЌНгDMЃЌгЩвбжЊЬѕМўвзжЄЁїABCЁеЁїDBMЃЌДгЖјПЩЕУAC=DMЃЌгЩДЫПЩЕУЕБDMЕФжЕзюДѓЪБЃЌACЕФжЕОЭзюДѓЃЌгЩЁЯBDC=90ЁуПЩжЊЕуDдквдBCЮЊжБОЖЕФ
ЃЛШчЭМ6ЃЌЕБЕуNдкBAЕФбгГЄЯпЩЯЪБЃЌЙ§ЕуPзїPEЁЭANгкЕуEЃЌгЩЁїAPNЪЧЕШбќжБНЧШ§НЧаЮЃЌAP=2ЃЌМДПЩЧѓЕУOEКЭPEЕФГЄЃЌДгЖјПЩЕУДЫЪБЕуPЕФзјБъЃЛЂкШчЯТЭМ7ЃЌвдBCЮЊБпзїЕШБпШ§НЧаЮЁїBCMЃЌСЌНгDMЃЌгЩвбжЊЬѕМўвзжЄЁїABCЁеЁїDBMЃЌДгЖјПЩЕУAC=DMЃЌгЩДЫПЩЕУЕБDMЕФжЕзюДѓЪБЃЌACЕФжЕОЭзюДѓЃЌгЩЁЯBDC=90ЁуПЩжЊЕуDдквдBCЮЊжБОЖЕФ![]() ЩЯдЫЖЏЃЌгЩЭМПЩжЊЕБDдкBCЩЯЗНЃЌЧвDMЁЭBCЪБЃЌDMЕФжЕзюДѓЃЌзюДѓжЕЮЊЃКЕШбќжБНЧЁїBDCаББпBCЩЯЕФИп+ЕШБпЁїBMCЕФИп.
ЩЯдЫЖЏЃЌгЩЭМПЩжЊЕБDдкBCЩЯЗНЃЌЧвDMЁЭBCЪБЃЌDMЕФжЕзюДѓЃЌзюДѓжЕЮЊЃКЕШбќжБНЧЁїBDCаББпBCЩЯЕФИп+ЕШБпЁїBMCЕФИп.
ЯъНтЃК
ЃЈ1ЃЉЁпЕуAЮЊЯпЖЮBCЭтвЛЖЏЕуЃЌЧв![]() ЃЌ
ЃЌ
ЁрЕБЕуAЮЛгкCBЕФбгГЄЯпЩЯЪБЃЌЯпЖЮACЕФГЄШЁЕУзюДѓжЕЃЌЧвзюДѓжЕЮЊ![]() ЃЌ
ЃЌ
ЙЪД№АИЮЊЃКCBЕФбгГЄЯпЩЯЃЌ ![]() ЃЛ
ЃЛ
![]() ЃЌ
ЃЌ
РэгЩЃКЁп![]() гы
гы![]() ЪЧЕШБпШ§НЧаЮЃЌ
ЪЧЕШБпШ§НЧаЮЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
МД![]() ЃЌ
ЃЌ
дк![]() гы
гы![]() жаЃЌ
жаЃЌ
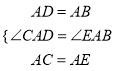 ЃЌ
ЃЌ
Ёр![]() Ёе
Ёе![]() ЃЌ
ЃЌ
Ёр![]() ЃЛ
ЃЛ
ЂкЁпЯпЖЮBEГЄЕФзюДѓжЕ![]() ЯпЖЮCDЕФзюДѓжЕЃЌ
ЯпЖЮCDЕФзюДѓжЕЃЌ
ЁргЩ![]() жЊЃЌЕБЯпЖЮCDЕФГЄШЁЕУзюДѓжЕЪБЃЌЕуDдкCBЕФбгГЄЯпЩЯЃЌ
жЊЃЌЕБЯпЖЮCDЕФГЄШЁЕУзюДѓжЕЪБЃЌЕуDдкCBЕФбгГЄЯпЩЯЃЌ
ЁрзюДѓжЕЮЊ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЂйШчЭМ5ЃЌСЌНгBMЃЌНЋ![]() ШЦзХЕуPЫГЪБеыа§зЊ
ШЦзХЕуPЫГЪБеыа§зЊ![]() ЕУЕН
ЕУЕН![]() ЃЌСЌНгANЃЌдђ
ЃЌСЌНгANЃЌдђ![]() ЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЪЧЕШбќжБНЧШ§НЧаЮЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёп![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌЕуBЕФзјБъЮЊ
ЃЌЕуBЕФзјБъЮЊ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрЯпЖЮAMГЄЕФзюДѓжЕ![]() ЯпЖЮBNГЄЕФзюДѓжЕЃЌ
ЯпЖЮBNГЄЕФзюДѓжЕЃЌ
ЁрЕБNдкЯпЖЮBAЕФбгГЄЯпЪБЃЌЯпЖЮBNШЁЕУзюДѓжЕЃЌ
зюДѓжЕ![]() ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ
ЁрзюДѓжЕЮЊ![]() ЃЛ
ЃЛ
ШчЭМ6ЃЌЙ§Pзї![]() жсгкEЃЌ
жсгкEЃЌ
Ёп![]() ЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЪЧЕШбќжБНЧШ§НЧаЮЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]()
ЂкШчЯТЭМ7ЃЌвдBCЮЊБпзїЕШБпШ§НЧаЮЁїBCMЃЌСЌНгDMЃЌ
Ёп![]() ЃЌ
ЃЌ
Ёр![]()
Ёп![]() ЃЌ
ЃЌ
Ёр![]() Ёе
Ёе![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁргћЧѓACЕФзюДѓжЕЃЌжЛвЊЧѓГіDMЕФзюДѓжЕМДПЩЃЌ
Ёп![]() ЖЈжЕЃЌ
ЖЈжЕЃЌ ![]() ЃЌ
ЃЌ
ЁрЕуDдквдBCЮЊжБОЖЕФ![]() ЩЯдЫЖЏЃЌ
ЩЯдЫЖЏЃЌ
гЩЭМЯѓПЩжЊЃЌЕБЕуDдкBCЩЯЗНЃЌDMЁЭBCЪБЃЌDMЕФжЕзюДѓЃЌзюДѓжЕ=ЕШбќжБНЧЁїBDCаББпЩЯЕФИп+ЕШБпЁїBCMЕФИпЃЌ
ЁпBC=![]() ЃЌ
ЃЌ
ЁрDMзюДѓ=![]() ЃЌ
ЃЌ
ЁрACзюДѓ=![]() ЃЎ
ЃЎ


 жЅТщПЊЛЈПЮГЬаТЬхбщЯЕСаД№АИ
жЅТщПЊЛЈПЮГЬаТЬхбщЯЕСаД№АИ дѕбљбЇКУХЃНђгЂгяЯЕСаД№АИ
дѕбљбЇКУХЃНђгЂгяЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
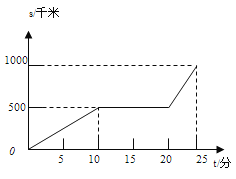
ЁОЬтФПЁПФГЬьдчГПЃЌЭѕРЯЪІДгМвГіЗЂВНааЧАЭљбЇаЃЃЌЭОжадкТЗБпвЛЗЙЕъГддчВЭЃЌШчЭМЫљЪОЪЧЭѕРЯЪІДгМвЕНбЇаЃетвЛЙ§ГЬжаЫљзпЕФТЗГЬSЃЈУзЃЉгыЪБМфt(Зж)жЎМфЕФЙиЯЕ.
ЃЈ1ЃЉбЇаЃРыЫћМв УзЃЌДгГіЗЂЕНбЇаЃЃЌЭѕРЯЪІЙВгУСЫ ЗжжгЃЛ
ЃЈ2ЃЉЭѕРЯЪІГддчВЭгУСЫЖрЩйЗжжгЃП
ЃЈ3ЃЉЭѕРЯЪІГддчВЭвдЧАЕФЫйЖШПьЛЙЪЧГдЭъдчВЭвдКѓЕФЫйЖШПьЃПГдЭъдчВЭКѓЕФЦНОљЫйЖШЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЪ§жсЩЯБъГіЕФЫљгаЕужаЃЌШЮвтЯрСкСНЕуМфЕФОрРыЯрЕШЃЌвбжЊЕуAБэЪОЉ12ЃЌЕуGБэЪО6ЃЎ
![]()
ЃЈ1ЃЉБэЪОдЕуЕФЕуЪЧЁЁЁЁЁЁЃЌЕуCБэЪОЕФЪ§ЪЧЁЁЁЁЁЁЁЁЃЛ
ЃЈ2ЃЉЪ§жсЩЯгаСНЕуMЁЂNЃЌЕуMЕНЕуDЕФОрРыЮЊ![]() ЃЌЕуNЕНЕуDЕФОрРыЮЊ4ЃЌЧѓЕуMЃЌNжЎМфЕФОрРыЃЛ
ЃЌЕуNЕНЕуDЕФОрРыЮЊ4ЃЌЧѓЕуMЃЌNжЎМфЕФОрРыЃЛ
ЃЈ3ЃЉЕуPЮЊЪ§жсЩЯвЛЕуЃЌЧвБэЪОЕФЪ§ЪЧећЪ§ЃЌЕуPЕНЕуAЕФОрРыгыЕуPЕНЕуGЕФОрРыжЎКЭЮЊ18ЃЌдђетбљЕФЕуPгаЁЁЁЁЁЁЁЁИіЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЩЬГЁОгЊФГжжЦЗХЦЕФЭцОпЃЌЙКНјЪБЕФЕЅМлЪЧ30дЊЃЌИљОнЪаГЁЕїВщЃКдквЛЖЮЪБМфФкЃЌЯњЪлЕЅМлЪЧ40дЊЪБЃЌЯњЪлСПЪЧ600МўЃЌЖјЯњЪлЕЅМлУПеЧ1дЊЃЌОЭЛсЩйЪлГі10МўЭцОпЃЎ
![]() ВЛЗСЩшИУжжЦЗХЦЭцОпЕФЯњЪлЕЅМлЮЊxдЊ
ВЛЗСЩшИУжжЦЗХЦЭцОпЕФЯњЪлЕЅМлЮЊxдЊ![]() ЃЌЧыФуЗжБ№гУxЕФДњЪ§ЪНРДБэЪОЯњЪлСПyМўКЭЯњЪлИУЦЗХЦЭцОпЛёЕУРћШѓwдЊЃЌВЂАбНсЙћЬюаДдкБэИёжаЃК
ЃЌЧыФуЗжБ№гУxЕФДњЪ§ЪНРДБэЪОЯњЪлСПyМўКЭЯњЪлИУЦЗХЦЭцОпЛёЕУРћШѓwдЊЃЌВЂАбНсЙћЬюаДдкБэИёжаЃК
ЯњЪлЕЅМл | x |
ЯњЪлСП | ______ |
ЯњЪлЭцОпЛёЕУРћШѓ | ______ |
![]() дк
дк![]() ЮЪЬѕМўЯТЃЌШєЩЬГЁЛёЕУСЫ10000дЊЯњЪлРћШѓЃЌЧѓИУЭцОпЯњЪлЕЅМлxгІЖЈЮЊЖрЩйдЊЃЎ
ЮЪЬѕМўЯТЃЌШєЩЬГЁЛёЕУСЫ10000дЊЯњЪлРћШѓЃЌЧѓИУЭцОпЯњЪлЕЅМлxгІЖЈЮЊЖрЩйдЊЃЎ
![]() дк
дк![]() ЮЪЬѕМўЯТЃЌШєЭцОпГЇЙцЖЈИУЦЗХЦЭцОпЯњЪлЕЅМлВЛЕЭгк44дЊЃЌЧвЩЬГЁвЊЭъГЩВЛЩйгк540МўЕФЯњЪлШЮЮёЃЌЧѓЩЬГЁЯњЪлИУЦЗХЦЭцОпЛёЕУЕФзюДѓРћШѓЪЧЖрЩйЃП
ЮЪЬѕМўЯТЃЌШєЭцОпГЇЙцЖЈИУЦЗХЦЭцОпЯњЪлЕЅМлВЛЕЭгк44дЊЃЌЧвЩЬГЁвЊЭъГЩВЛЩйгк540МўЕФЯњЪлШЮЮёЃЌЧѓЩЬГЁЯњЪлИУЦЗХЦЭцОпЛёЕУЕФзюДѓРћШѓЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯп![]() гыxжсНЛгкAЁЂBСНЕуЃЌЦфжаЕу
гыxжсНЛгкAЁЂBСНЕуЃЌЦфжаЕу![]() ЃЌНЛyжсгкЕу
ЃЌНЛyжсгкЕу![]() жБЯп
жБЯп![]() Й§ЕуBгыyжсНЛгкЕуNЃЌгыХзЮяЯпЕФСэвЛИіНЛЕуЪЧDЃЌЕуPЪЧжБЯпBDЯТЗНЕФХзЮяЯпЩЯвЛЖЏЕу
Й§ЕуBгыyжсНЛгкЕуNЃЌгыХзЮяЯпЕФСэвЛИіНЛЕуЪЧDЃЌЕуPЪЧжБЯпBDЯТЗНЕФХзЮяЯпЩЯвЛЖЏЕу![]() ВЛгыЕуBЁЂDжиКЯ
ВЛгыЕуBЁЂDжиКЯ![]() ЃЌЙ§ЕуPзїyжсЕФЦНааЯпЃЌНЛжБЯпBDгкЕуEЃЌЙ§ЕуDзї
ЃЌЙ§ЕуPзїyжсЕФЦНааЯпЃЌНЛжБЯпBDгкЕуEЃЌЙ§ЕуDзї![]() жсгкЕуMЃЎ
жсгкЕуMЃЎ
![]() ЧѓХзЮяЯп
ЧѓХзЮяЯп![]() ЕФБэДяЪНМАЕуDЕФзјБъЃЛ
ЕФБэДяЪНМАЕуDЕФзјБъЃЛ
![]() ШєЫФБпаЮPEMNЪЧЦНааЫФБпаЮЃПЧыЧѓГіЕуPЕФзјБъЃЛ
ШєЫФБпаЮPEMNЪЧЦНааЫФБпаЮЃПЧыЧѓГіЕуPЕФзјБъЃЛ
![]() Й§ЕуPзї
Й§ЕуPзї![]() гкЕуFЃЌЩш
гкЕуFЃЌЩш![]() ЕФжмГЄЮЊCЃЌЕуPЕФКсзјБъЮЊaЃЌЧѓCгыaЕФКЏЪ§ЙиЯЕЪНЃЌВЂЧѓГіCЕФзюДѓжЕЃЎ
ЕФжмГЄЮЊCЃЌЕуPЕФКсзјБъЮЊaЃЌЧѓCгыaЕФКЏЪ§ЙиЯЕЪНЃЌВЂЧѓГіCЕФзюДѓжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊжБЯпy=Љ![]() x+3гызјБъжсЗжБ№НЛгкЕуAЃЌBЃЌЕуPдкХзЮяЯпy=ЉЃЈxЉ
x+3гызјБъжсЗжБ№НЛгкЕуAЃЌBЃЌЕуPдкХзЮяЯпy=ЉЃЈxЉ![]() ЃЉ2+4ЩЯЃЌФмЪЙЁїABPЮЊЕШбќШ§НЧаЮЕФЕуPЕФИіЪ§гаЃЈЁЁЁЁЃЉ
ЃЉ2+4ЩЯЃЌФмЪЙЁїABPЮЊЕШбќШ§НЧаЮЕФЕуPЕФИіЪ§гаЃЈЁЁЁЁЃЉ
A. 8Иі B. 4Иі C. 5Иі D. 6Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌжБЯпy=Љ3x+3гыxжсЁЂyжсЗжБ№НЛгкAЁЂBСНЕуЃЌвдABЮЊБпдкЕквЛЯѓЯозїе§ЗНаЮABCDбиxжсИКЗНЯђЦНвЦaИіЕЅЮЛГЄЖШКѓЃЌЕуCЧЁКУТфдкЫЋЧњЯпЩЯЃЌдђaЕФжЕЪЧ ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєДњЪ§ЪНЃЈ2x2+axЉy+6ЃЉЉЃЈ2bx2Љ3x+5yЉ1ЃЉЕФжЕгызжФИxЫљШЁЕФжЕЮоЙиЃЌДњЪ§ЪН![]() a2Љ2b2ЉЃЈ
a2Љ2b2ЉЃЈ![]() a3Љ3b2ЃЉЃН_____
a3Љ3b2ЃЉЃН_____
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЙЋЫОаТбаЗЂвЛжжАьЙЋЪвгУБкЙвЪНЕчДХШеРњЃЌЕзАхЪЧвЛПщГЄЗНаЮДХПщЃЌдйгУ31УЖдВжљаЮаЁЬњЦЌБъЩЯЪ§зжЮќИНдкЕзАхЩЯзїЮЊШеЦкЃЌШчЭМ1ЪЧ2007Фъ10дТЗнШеРњ
ЃЈ1ЃЉгУГЄЗНаЮКЭе§ЗНаЮЗжБ№ШІГіЯрСкЕФ3ИіЪ§КЭ9ИіЪ§ЃЌШєЩшШІГіЕФЪ§ЕФжааФЪ§ЮЊaЃЌгУКЌaЕФећЪНБэЪОет3ИіЪ§ЕФКЭгы9ИіЪ§ЕФКЭЃЌНсЙћЗжБ№ЮЊЁЁ ЁЁЃЌЁЁ ЁЁЃЎ
ЃЈ2ЃЉгУФГжжЭМаЮШІГіЯрСкЕФ5ИіЪ§ЃЌЪЙет5ИіЪ§ЕФКЭФмБэЪОГЩ5aЕФаЮЪНЃЌЧыдкЭМ2жаЛГівЛИіетбљЕФЭМаЮЃЎ
ЃЈ3ЃЉгУЦНааЫФБпаЮШІГіЯрСкЕФЫФИіЪ§ЃЌЪЧЗёДцдкетбљЕФ4ИіЪ§ЪЙЕУa+b+c+dЃН114ЃПШчЙћДцдкОЭЧѓГіРДЃЌВЛДцдкЫЕУїРэгЩЃЎ
ЃЈ4ЃЉЕквЛДЮЗЖЏ31УЖШеРњЬњЦЌЃЌЕкЖўДЮЗЖЏЦфжаЕФ30УЖЃЌЕкШ§ДЮЗЖЏЦфжаЕФ29УЖЃЌЁЁЃЌЕк31ДЮжЛЗЖЏЦфжаЕФвЛУЖЃЌАДетбљЕФЗНЗЈЗЖЏШеРњЬњЦЌЃЌФмЗёЪЙЬњАхЩЯЫљгаЕФ31УЖЬњЦЌдРДгаЪ§зжЕФвЛУцЖМГЏЯТЃЌЪдЭЈЙ§МЦЫужЄУїФуЕФХаЖЯЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com