
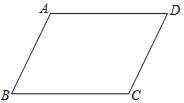
【题目】如图,已知四边形ABCD是平行四边形,AB<AD.
(1)利用尺规作图作出∠ABC的角平分线BG,交AD于点E,记点A关于BE对称点为F(要求保留作图痕迹,不写作法);
(2)在(1)所作的图中,若AF=6,AB=5,求BE的长和四边形ABFE的面积.
【答案】(1)详见解析;(2)24.
【解析】
(1)根据角平分线的作法作出∠ABC的平分线即可;
(2)首先根据角平分线的性质以及平行线的性质得出∠ABE=∠AEB,进而得出△ABO≌△FBO,进而利用AF⊥BE,BO=EO,AO=FO,得出即可.
(1)∠ABC的平分线AG,交AD于点E,作AF⊥BE交AD于F,则点A、F关于BE对称,如图所示,
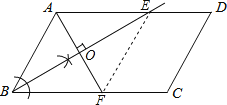
(2)设AF与BE交于点O,
∵BE垂直平分AF,
∴AO=![]() AF=3,
AF=3,
在Rt△AOB中,∵∠AOB=90°,AB=5,AO=3,
∴BO=![]() =4,
=4,
∴BE=2BO=8
∵四边形ABCD是平行四边形,
∴AE∥BF,
∴∠DAF=∠AFB=∠BAF,
∴BA=BF,
∴四边形ABEF是菱形.
∴S四边形ABEF=![]() ×AF×BE=
×AF×BE=![]() ×6×8=24
×6×8=24


科目:初中数学 来源: 题型:
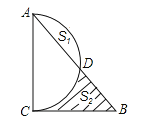
【题目】以△ABC的边AC为直径的半圆交AB边于D点,∠A、∠B、∠C所对边长为a、b、c,且二次函数y=![]() (a+c)x2-bx+
(a+c)x2-bx+![]() (c-a)顶点在x轴上,a是方程z2+z-20=0的根.
(c-a)顶点在x轴上,a是方程z2+z-20=0的根.
(1)证明:∠ACB=90°;
(2)若设b=2x,弓形面积S弓形AED=S1,阴影面积为S2,求(S2-S1)与x的函数关系式;
(3)在(2)的条件下,当BD为何值时,(S2-S1)最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
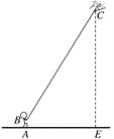
【题目】小明在海湾森林公园放风筝.如图所示,小明在A处,风筝飞到C处,此时线长BC为40米,若小明双手牵住绳子的底端B距离地面1.5米,从B处测得C处的仰角为60°,求此时风筝离地面的高度CE.(计算结果精确到0.1米,![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农经公司以40元/千克的价格收购一批农产品进行销售,经过市场调查,发现该产品日销售量p(千克)与销售价格x(元/千克)之间满足一次函数关系,部分数据如表:
销售价格x(元/千克) | 40 | 50 | 60 | 70 | 80 |
日销售量p (千克) | 120 | 100 | 80 | 60 | 40 |
(1)求p与x之间的函数表达式;
(2)农经公司应该如何确定这批农产品的销售价格,才能使日销售利润最大?
(3)若农经公司每销售1千克这种农产品需支出m元(m>0)的相关费用,当![]() 时,农经公司的日获利的最大值为1682元,求m的值.(日获利日销售利润日支出费用)
时,农经公司的日获利的最大值为1682元,求m的值.(日获利日销售利润日支出费用)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将等腰三角形![]() 折叠,使顶点
折叠,使顶点![]() 与底边
与底边![]() 的中点
的中点![]() 重合,折线分别交
重合,折线分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,连接
,连接![]() 、
、![]() .
.
(1)如图1,求证:四边形![]() 是菱形;
是菱形;
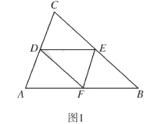
(2)如图2,延长![]() 至点
至点![]() ,使
,使![]() ,连接
,连接![]() ,并延长
,并延长![]() 交
交![]() 的延长线于点
的延长线于点![]() ,在不添加任何辅助线的情况下,请直接写出图2中的所有平行四边形(不包括以
,在不添加任何辅助线的情况下,请直接写出图2中的所有平行四边形(不包括以![]() 为一边的平行四边形)
为一边的平行四边形)

查看答案和解析>>
科目:初中数学 来源: 题型:
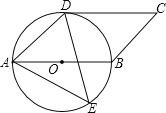
【题目】如图,四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,E是⊙O上一点,且∠AED=45°.
(1)试判断CD与⊙O的位置关系,并证明你的结论;
(2)若⊙O的半径为3,sin∠ADE=![]() ,求AE的值.
,求AE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在中俄“海上联合—2014”反潜演习中,我军舰A测得潜艇C的俯角为300.位于军舰A正上方1000米的反潜直升机B侧得潜艇C的俯角为680,试根据以上数据求出潜艇C离开海平面的下潜深度。(结果保留整数。参考数据:sin680≈0.9,cos680≈0.4,,tan680≈2.5. ![]() ≈1.7)
≈1.7)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰![]() ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的垂直平分线交于点O、点C沿EF折叠后与点O重合,则∠CEF的度数是( )
ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的垂直平分线交于点O、点C沿EF折叠后与点O重合,则∠CEF的度数是( )
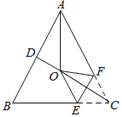
A. 60° B. 55° C. 50° D. 45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“南昌之星”摩天轮,位于江西省南昌市红谷滩新区红角洲赣江边上的赣江市民公园,摩天轮高![]() (最高点到地面的距离).如图,点
(最高点到地面的距离).如图,点![]() 是摩天轮的圆心,
是摩天轮的圆心,![]() 是其垂直于地面的直径,小贤在地面点
是其垂直于地面的直径,小贤在地面点![]() 处利用测角仪测得摩天轮的最高点
处利用测角仪测得摩天轮的最高点![]() 的仰角为
的仰角为![]() ,测得圆心
,测得圆心![]() 的仰角为
的仰角为![]() ,则摩天轮的半径为________
,则摩天轮的半径为________![]() (结果保留
(结果保留![]() ).
).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com