
【题目】如图,平面直角坐标系中,已知点A(﹣1,2),B(﹣2,0),C(﹣4,1),把三角形ABC向上平移1个单位长度,向右平移5个单位长度,可以得到三角形A′B′C′.
(Ⅰ)在图中画出△A′B′C′;
(Ⅱ)直接写出点A′、B′、C′的坐标;
(Ⅲ)写出A′C′与AC之间的位置关系和大小关系.

 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=mx2﹣8mx+4m+2(m>0)与y轴的交点为A,与x轴的交点分别为B(x1 , 0),C(x2 , 0),且x2﹣x1=4,直线AD∥x轴,在x轴上有一动点E(t,0)过点E作平行于y轴的直线l与抛物线、直线AD的交点分别为P、Q.
(1)求抛物线的解析式;
(2)当0<t≤8时,求△APC面积的最大值;
(3)当t>2时,是否存在点P,使以A、P、Q为顶点的三角形与△AOB相似?若存在,求出此时t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD边长为2,AB∥x轴,AD∥y轴,顶点A恰好落在双曲线y= ![]() 上,边CD,BC分别交双曲线于E,F两点,若线段AE过原点,则EF的长为( )
上,边CD,BC分别交双曲线于E,F两点,若线段AE过原点,则EF的长为( ) 
A.1
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 如图
如图![]() 所示,在
所示,在![]() 中,
中,![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() ,求证:
,求证:![]() 的周长
的周长![]() ;21.
;21.
![]() 如图
如图![]() 所示,在
所示,在![]() 中,若
中,若![]() ,
,![]() ,
,![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() ,试判断
,试判断![]() 的形状,并证明你的结论.
的形状,并证明你的结论.
![]() 如图
如图![]() 所示,在
所示,在![]() 中,若
中,若![]() ,
,![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,
,![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长.
的长.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图中的图像(折线ABCDE)描述了一汽车在某一直线上的行驶过程中,汽车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系,根据图中提供的信息,给出下列说法:①汽车共行驶了120千米;②汽车在行驶途中停留了0.5小时;③汽车在整个行驶过程中的平均速度为80.8千米/时;④汽车自出发后3小时至4.5小时之间行驶的速度在逐渐减小.⑤汽车离出发地64千米是在汽车出发后1.2小时时。其中正确的说法共有( )

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车专买店销售A,B两种型号的新能源汽车,上周售出1辆A型车和3辆B型车,销售额为96万元;本周已售出2辆A型车和1辆B型车,销售额为62万元.
(1)求每辆A型车和B型车的件价各为多少万元;
每辆A型车和B型车的售价分别是x万元,y万元.
根据题意,列方程组
解这个方程组,得x= ,y=
答: .
(2)有一家公司拟向该店购买A,B两种型号的新能源汽车共6辆,购车费不超过130万元,求这次购进B型车最多几辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,A(﹣2,0),C(2,2),过C作CB⊥x轴于B.

(1)如图1,△ABC的面积是 ;
(2)如图1,在y轴上找一点P,使得△ABP的面积与△ABC的面积相等,请直接写出P点坐标: ;
(3)如图2,若过B作BD∥AC交y轴于D,则∠BAC+∠ODB的度数为 度;
(4)如图3,BD∥AC,若AE、DE分别平分∠CAB,∠ODB,求∠AED的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①a+b+c<0;②a﹣b+c<0;③b+2a<0;④abc>0,其中正确的是(填编号) 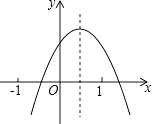
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com