
 ��ͼ����֪A��B������ֱ��AB��x��������ᣬy���������Ľ��㣬��OA��OB�ij��ֱ���x2-14x+48=0����������OA��OB��������BCƽ�֡�ABO��x����C�㣬����һ����P��ÿ��1����λ���ٶȴ�B�㿪ʼ������BC�ƶ����˶�ʱ��Ϊt�룮
��ͼ����֪A��B������ֱ��AB��x��������ᣬy���������Ľ��㣬��OA��OB�ij��ֱ���x2-14x+48=0����������OA��OB��������BCƽ�֡�ABO��x����C�㣬����һ����P��ÿ��1����λ���ٶȴ�B�㿪ʼ������BC�ƶ����˶�ʱ��Ϊt�룮���� ��1���ⷽ��x2-14x+48=0���ɵõ������
��2�����ݽ�ƽ���ߵ����ʵõ�P�ǽ�ƽ�����ϵĵ㣬P��OB��AB�ľ�����ȣ������������εĸ���ȣ�S1��S2=AB��OB=5��3��
��3����C��CD��ֱAB������ΪD��OC=x����CD=x����֪BD=OB�����ݹ��ɶ����з������C������꣨3��0�����õ�ֱ��BC�Ľ���ʽ��y=-2x+6��Ȼ������������һ���ٵ�BP=OB=6ʱ���õ�t=6���ڵ�BP=OPʱ��P��OB���д����ϣ��õ�yp=3������ֱ��BC�Ľ���ʽ��P��$\frac{3}{2}$��3�������ù��ɶ����ɵ�BP=$\frac{3\sqrt{5}}{2}$�����ɵõ�t��ֵ���۵�OB=OP=6ʱ����P��m��-2m+6�������ݹ��ɶ����з���m2+��-2m+6��2=62�����m=$\frac{24}{5}$��Ȼ���ٸ��ݹ��ɶ����õ�PB=$\sqrt{��\frac{24}{5}��^{2}+��\frac{48}{5}��^{2}}$=$\frac{24\sqrt{5}}{5}$����ý����
��� �⣺��1����OA��OB�ij��Ƿ���x2-14x+48=0��������OA��OB����
�ⷽ�̵ã�x1=8��x2=6��
��OA��OB��
��OA=8��OB=6��
��2����ͼ1 ����P����PD��BO��PH��AB������ֱ�ΪD��H��
����P����PD��BO��PH��AB������ֱ�ΪD��H��
��BCΪ��ABO��ƽ���ߣ�
��PH=PD��
��S1��S2=AB��OB��
��OA=8��OB=6��
��AB=10��
��S1��S2=AB��OB=5��3��
��3����ͼ3����C��CD��ֱAB������ΪD��
��OC=x����CD=x����֪BD=OB��
��ֱ��������CDA�У�CD2+AD2=AC2��
��x2+42=��8-x��2��
��ã�x=3��
����C������꣨3��0����
��ֱ��BC�Ľ���ʽ��y=-2x+6��
��BP=OBʱ��t=6��
��BP=OPʱ��P��OB���д����ϣ�yp=3������ֱ��BC�Ľ���ʽ��P��$\frac{3}{2}$��3����
���ù��ɶ����ɵ�BP=$\frac{3\sqrt{5}}{2}$��
��t=$\frac{3\sqrt{5}}{2}$��
��OB=OP=6ʱ����P��m��-2m+6����
����ݹ��ɶ����ã�m2+��-2m+6��2=62��
��ã�m=$\frac{24}{5}$��
��PB=$\sqrt{��\frac{24}{5}��^{2}+��\frac{48}{5}��^{2}}$=$\frac{24\sqrt{5}}{5}$��
��t=$\frac{24\sqrt{5}}{5}$��
���� ���⿼���˽�һԪ���η��̣���ƽ���ߵ����ʣ����ɶ����������Ľ���ʽ����ȷ�Ļ����������ǽ���Ĺؼ���


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
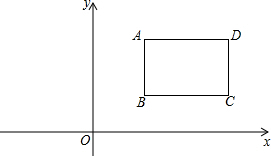 ��ƽ��ֱ������ϵ�͵�һ��������һ����ABCD��ADƽ����x�ᣬ���е�A��3��4����AB=2��BC=3����������ABCD����ƽ��a����λ֮���ε��˵ڶ����ޣ���ʱB��D������ͬһ˫����y=$\frac{k}{x}$�ϣ�
��ƽ��ֱ������ϵ�͵�һ��������һ����ABCD��ADƽ����x�ᣬ���е�A��3��4����AB=2��BC=3����������ABCD����ƽ��a����λ֮���ε��˵ڶ����ޣ���ʱB��D������ͬһ˫����y=$\frac{k}{x}$�ϣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
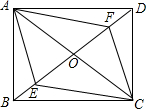 ��ͼ���ı���ABCD�ĶԽ���AC��BD���ڵ�O����֪O��BD���е㣬BE=DF��AF��CE��
��ͼ���ı���ABCD�ĶԽ���AC��BD���ڵ�O����֪O��BD���е㣬BE=DF��AF��CE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
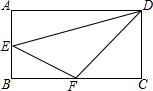 ��ͼ���ڳ�����ABCD�У�AB=4cm��BC=8cm��E��F�ֱ���AB��BC���е㣮��E��DF�ľ�����3$\sqrt{2}$cm��
��ͼ���ڳ�����ABCD�У�AB=4cm��BC=8cm��E��F�ֱ���AB��BC���е㣮��E��DF�ľ�����3$\sqrt{2}$cm���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
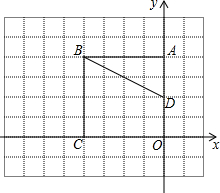 ��ͼ����ֱ������ϵ�У�A��0��4����B��-4��4����C��-4��0����D��0��2����
��ͼ����ֱ������ϵ�У�A��0��4����B��-4��4����C��-4��0����D��0��2�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com