
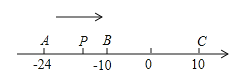
【题目】已知数轴上有A、B、C三个点,分别表示有理数-24,-10,10,动点P从A出发,以每秒1个单位的速度向终点C移动,设移动时间为t秒.
(1)用含t的代数式表示P到点A和点C的距离:PA= ,PC= .
(2)当点P运动到B点时,点Q从A点出发,以每秒3个单位的速度向C点运动,Q点到达C点后,再立即以同样的速度返回,运动到终点A.
①在运动过程中,t为何值时P与Q重合?
②在点Q开始运动后,P、Q两点之间的距离能否为2个单位?如果能,请求出此时点P表示的数;如果不能,请说明理由.
【答案】(1)t,34-t;(2)①21或![]() ;②t为20、22、27、28时,PQ=2..点P表示的数分别为:4,2,3,4.
;②t为20、22、27、28时,PQ=2..点P表示的数分别为:4,2,3,4.
【解析】试题分析:(1)数轴上求距离,利用大的(右边)坐标减去小的(左边)坐标,或者任意两个坐标作差再求绝对值. (2)根据题意求解绝对值方程.
试题解析:
解:(1)PA=t,PC=34-t,(2)①21或![]()
②P从A到B需要时间:14秒,QA=3(t14),当Q从A到C过程:PQ=|t3(t14)|=|422t|=2,422t=2得,t=20,422t=2得,t=22,当Q从C往回,Q到达C需要时间: ![]() , CQ=3(t14
, CQ=3(t14![]() )=3t76,PQ=|34t(3t76)|=|1104t|=2,1104t=±2,t=27或t=28.
)=3t76,PQ=|34t(3t76)|=|1104t|=2,1104t=±2,t=27或t=28.
答:t为20、22、27、28时,PQ=2.
点P表示的数分别为:4;2;3;4.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,AC为矩形ABCD的对角线,将边AB沿AE折叠,使点B落在AC上的点M处,将边CD沿CF折叠,使点D落在AC上的点N处,若AB=6cm,AC=10cm,则四边形AECF的面积为cm2.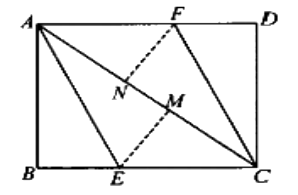
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如图(1),若分别以△ABC的三边AC,BC,AB为边向三角形外侧作正方形ACDE,BCFG和ABMN,则称这三个正方形为△ABC的外展三叶正方形,其中任意两个正方形为△ABC的外展双叶正方形. 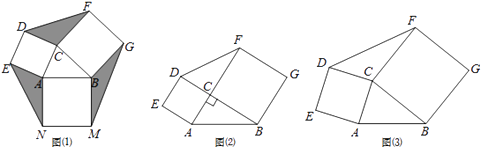
(1)作△ABC的外展双叶正方形ACDE和BCFG,记△ABC,△DCF的面积分别为S1和S2 . ①如图(2),当∠ACB=90°时,求证:S1=S2 .
②如图(3),当∠ACB≠90°时,S1与S2是否仍然相等,请说明理由.
(2)已知△ABC中,AC=3,BC=4,作其外展三叶正方形,记△DCF,△AEN,△BGM的面积和为S,请利用图(1)探究:当∠ACB的度数发生变化时,S的值是否发生变化?若不变,求出S的值;若变化,求出S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
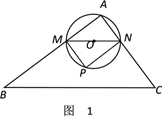
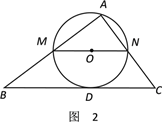
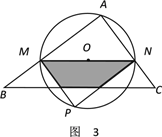
【题目】在△ABC中,∠A=90°,AB=4,AC=3,M是AB上的动点(不与A,B重合),过M点作MN∥BC交AC于点N.以MN为直径作⊙O,并在⊙O内作内接矩形AMPN.令AM=x.
(1)用含x的代数式表示△MNP的面积S;
(2)当x为何值时,⊙O与直线BC相切?
(3)在动点M的运动过程中,记△MNP与梯形BCNM重合的面积为y,试求y关于x的函数表达式,并求x为何值时,y的值最大,最大值是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com