
【题目】如图,点O在直线AB上,OC⊥OD,∠EDO与∠1互余.
(1)求证:ED//AB;
(2)OF平分∠COD交DE于点F,若∠OFD=65°,补全图形,并求∠1的度数.

 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:
【题目】对于正数![]() ,用符号
,用符号![]() 表示
表示![]() 的整数部分,例如:
的整数部分,例如:![]() ,
,![]() ,
,![]() .点
.点![]() 在第一象限内,以A为对角线的交点画一个矩形,使它的边分别与两坐标轴垂直. 其中垂直于
在第一象限内,以A为对角线的交点画一个矩形,使它的边分别与两坐标轴垂直. 其中垂直于![]() 轴的边长为
轴的边长为![]() ,垂直于
,垂直于![]() 轴的边长为
轴的边长为![]() ,那么,把这个矩形覆盖的区域叫做点A的矩形域.例如:点
,那么,把这个矩形覆盖的区域叫做点A的矩形域.例如:点![]() 的矩形域是一个以
的矩形域是一个以![]() 为对角线交点,长为3,宽为2的矩形所覆盖的区域,如图1所示,它的面积是6.
为对角线交点,长为3,宽为2的矩形所覆盖的区域,如图1所示,它的面积是6.


图1 图2
根据上面的定义,回答下列问题:
(1)在图2所示的坐标系中画出点 的矩形域,该矩形域的面积是 ;
(2)点![]() 的矩形域重叠部分面积为1,求
的矩形域重叠部分面积为1,求![]() 的值;
的值;
(3)已知点![]() 在直线
在直线![]() 上, 且点B的矩形域的面积
上, 且点B的矩形域的面积![]() 满足
满足![]() ,那么
,那么![]() 的取值范围是 .(直接写出结果)
的取值范围是 .(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司招聘职员两名,对甲、乙、丙、丁四名候选人进行了笔试和面试,各项成绩满分均为100分,然后再按笔试占60%、面试占40%计算候选人的综合成绩(满分为100分).
他们的各项成绩如下表所示:
修造人 | 笔试成绩/分 | 面试成绩/分 |
甲 | 90 | 88 |
乙 | 84 | 92 |
丙 | x | 90 |
丁 | 88 | 86 |
(1)直接写出这四名候选人面试成绩的中位数;
(2)现得知候选人丙的综合成绩为87.6分,求表中x的值;
(3)求出其余三名候选人的综合成绩,并以综合成绩排序确定所要招聘的前两名的人选.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学有一块四边形的空地ABCD,如图所示,为了绿化环境,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,DA=4m,BC=12m,CD=13m.
(1)求出空地ABCD的面积.
(2)若每种植1平方米草皮需要200元,问总共需投入多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形![]() 中,
中,![]() ,
,![]() 为
为![]() 上一动点,
上一动点,![]() 交
交![]() 于
于![]() ,过
,过![]() 作
作![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,过
,过![]() 作
作![]() 于
于![]() ,下列有四个结论:①
,下列有四个结论:①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() 的周长为定值,其中正确的结论有( ).
的周长为定值,其中正确的结论有( ).

A.①②③B.①②④C.①③④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
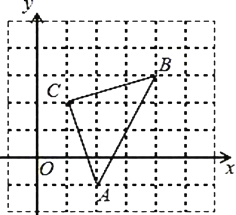
【题目】如图,平面直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2).
(1)写出点A、B的坐标:A ,B ;
(2)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A1B1C1,画出△A1B1C1;
(3)若AB边上有一点M(a,b),平移后对应的点M1的坐标为________________;
(4)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形 ABCD中AB= 3,点B在边CD上,且 CD=3DE. 将△ADE沿AE对折至△AFE,延长EF交边BC 于点G,连接AG,CF下列结论:①点G是BC的中点;②FG=FC;③![]() GAE=45;④GE=BG+DE.其中正确的是( )
GAE=45;④GE=BG+DE.其中正确的是( )

A. ①② B. ①③④ C. ②③ D. ①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com