
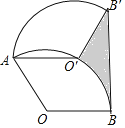
【题目】如图,将半径为2,圆心角为![]() 的扇形
的扇形![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,点
,点![]() 、
、![]() 的对应点分别为
的对应点分别为![]() ,
,![]() ,连接
,连接![]() ,则图中阴影部分的面积是( )
,则图中阴影部分的面积是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】分析:连接OO′,BO′,根据旋转的性质得到∠OAO′=60°,推出△OAO′是等边三角形,得到∠AOO′=60°,推出△OO′B是等边三角形,得到∠AO′B=120°,得到∠O′B′B=∠O′BB′=30°,根据图形的面积公式即可得到结论.
详解:连接OO′,BO′.

∵将半径为2,圆心角为120°的扇形OAB绕点A逆时针旋转60°,
∴∠OAO′=60°,
∴△OAO′是等边三角形,
∴∠AOO′=60°,
∵∠AOB=120°,
∴∠O′OB=60°,
∴△OO′B是等边三角形,
∴∠AO′B=120°,
∵∠AO′B′=120°,
∴∠B′O′B=120°,
∴∠O′B′B=∠O′BB′=30°,
∴∠OBB′=90°,
∴BB′=![]() =2
=2![]() .
.
∴图中阴影部分的面积=S△B′OB-S扇形OO′B=![]() .
.
故选C.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
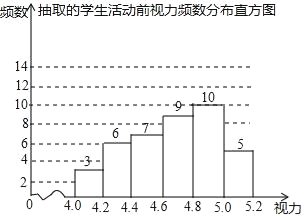
【题目】为了保护视力,学校开展了全校性的视力保健活动,活动前,随机抽取部分学生,检查他们的视力,结果如图所示(数据包括左端点不包括右端点,精确到0.1);活动后,再次检查这部分学生的视力,结果如表所示
分组 | 频数 |
4.0≤x<4.2 | 2 |
4.2≤x<4.4 | 3 |
4.4≤x<4.6 | 5 |
4.6≤x<4.8 | 8 |
4.8≤x<5.0 | 17 |
5.0≤x<5.2 | 5 |
(1)求活动所抽取的学生人数;
(2)若视力达到4.8及以上为达标,计算活动前该校学生的视力达标率;
(3)请选择适当的统计量,从两个不同的角度评价视力保健活动的效果.
查看答案和解析>>
科目:初中数学 来源: 题型:
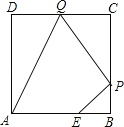
【题目】如图,已知正方形ABCD边长为3,点E在AB边上且BE=1,点P,Q分别是边BC,CD的动点(均不与顶点重合),当四边形AEPQ的周长取最小值时,四边形AEPQ的面积是( )
A. 3 B. 5 C. 4 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①若a,b互为相反数,则![]() =-1;②若a+b<0,ab>0,则|a+2b|=-a-2b;③若多项式ax3+bx+1的值为5,则多项式-ax3-bx+1的值为-3;④若甲班有50名学生,平均分是a分,乙班有40名学生,平均分是b分,则两班的平均分为
=-1;②若a+b<0,ab>0,则|a+2b|=-a-2b;③若多项式ax3+bx+1的值为5,则多项式-ax3-bx+1的值为-3;④若甲班有50名学生,平均分是a分,乙班有40名学生,平均分是b分,则两班的平均分为![]() 分.其中正确的为____(填序号).
分.其中正确的为____(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2+(m﹣3)x﹣m(2m﹣3)=0
(1)证明:无论m为何值方程都有两个实数根;
(2)是否存在正数m,使方程的两个实数根的平方和等于26?若存在,求出满足条件的正数m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
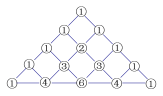
【题目】在我国南宋数学家杨辉(约13世纪)所著的《详解九章算术》(1261年)一书中,用下图的三角形解释二项和的乘方规律.杨辉在注释中提到,在他之前北宋数学家贾宪(1050年左右)也用过上述方法,因此我们称这个三角形为“杨辉三角”或“贾宪三角”.杨辉三角两腰上的数都是![]() ,其余每一个数为它上方(左右)两数的和.事实上,这个三角形给出了
,其余每一个数为它上方(左右)两数的和.事实上,这个三角形给出了![]()
![]() 的展开式(按
的展开式(按![]() 的次数由大到小的顺序)的系数规律.例如,此三角形中第三行的
的次数由大到小的顺序)的系数规律.例如,此三角形中第三行的![]() 个数
个数![]() ,恰好对应着
,恰好对应着![]() 展开式中的各项系数,第四行的
展开式中的各项系数,第四行的![]() 个数
个数![]() ,恰好对应着
,恰好对应着![]() 展开式中的各项系数,等等.请依据上面介绍的数学知识,解决下列问题:
展开式中的各项系数,等等.请依据上面介绍的数学知识,解决下列问题:
(1)写出![]() 的展开式;
的展开式;
(2)利用整式的乘法验证你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
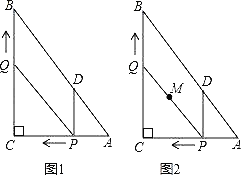
【题目】如图1,在Rt△ABC中,∠C=90°,AC=6,BC=8,动点P从点A开始沿边AC向点C以1个单位长度的速度运动,动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动,过点P作PD∥BC,交AB于点D,连接PQ分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒(t≥0).
(1)直接用含t的代数式分别表示:QB= ,PD= .
(2)是否存在t的值,使四边形PDBQ为菱形?若存在,求出t的值;若不存在,说明理由.并探究如何改变Q的速度(匀速运动),使四边形PDBQ在某一时刻为菱形,求点Q的速度;
(3)如图2,在整个运动过程中,求出线段PQ中点M所经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂制作甲、乙两种环保包装盒,已知同样用6m材料制成甲盒的个数比制成乙盒的个数少2个,且制成一个甲盒比制成一个乙盒需要多用20%的材料.
(1)求制作每个甲盒、乙盒各用多少米材料?
(2)如果制作甲、乙两种包装盒共3000个,且甲盒的数量不少于乙盒数量的2倍,那么请写出所需要材料的总长度l(m)与甲盒数量n(个)之间的函数关系式,并求出最少需要多少米材料?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】蜗牛从某点O开始沿东西方向直线爬行,规定向东爬行的路程记为正数,向西爬行的路程记为负数.爬行的各段路程依次为(单位:厘米):![]() .问:
.问:
(1)蜗牛最后是否回到出发点O?
(2)蜗牛离开出发点O最远是多少厘米?
(3)在爬行过程中,如果每爬行1厘米奖励一粒芝麻,则蜗牛可得到多少粒芝麻?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com