
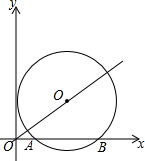 在平面直角坐标系中,⊙O′与x轴相交于A(2,0),B(8,0),⊙O′的圆心O′在直线y=$\frac{4}{5}$x上,求⊙O′的半径,并判断⊙O′与y轴的位置关系.
在平面直角坐标系中,⊙O′与x轴相交于A(2,0),B(8,0),⊙O′的圆心O′在直线y=$\frac{4}{5}$x上,求⊙O′的半径,并判断⊙O′与y轴的位置关系. 分析 作O′C⊥AB于C,连接O′B,则∠O′CB=90°,由已知条件得出OA=2,OB=8,AB=8-2=6,由垂径定理得出AC=BC=$\frac{1}{2}$AB=3,求出点O′的坐标为(5,4),O′C=4,由勾股定理得出O′B=$\sqrt{O′{C}^{2}+B{C}^{2}}$=5,即可得出⊙O′的半径为5;由圆心O′到y轴的距离=⊙O′的半径,得出⊙O′与y轴相切.
解答 解:作O′C⊥AB于C,连接O′B,如图所示: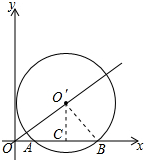
则∠O′CB=90°,
∵A(2,0),B(8,0),
∴OA=2,OB=8,
∴AB=8-2=6,
由垂径定理得:AC=BC=$\frac{1}{2}$AB=3,
∴OC=2+3=5,
把x=5代入直线y=$\frac{4}{5}$x得:y=4,
∴点O′的坐标为(5,4),O′C=4,
由勾股定理得:O′B=$\sqrt{O′{C}^{2}+B{C}^{2}}$=$\sqrt{{4}^{2}+{3}^{2}}$=5,
即⊙O′的半径为5;
∵点O′的坐标为(5,4),
∴圆心O′到y轴的距离d=5=⊙O′的半径,
∴⊙O′与y轴的位置关系是相切.
点评 本题考查了直线与圆的位置关系、勾股定理、垂径定理、一次函数图象上点的坐标特征;通过作辅助线运用垂径定理和勾股定理是解决问题的关键.


 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:解答题
| 数量(册) | 售价(元) |
| 100 | 200+200×0.15 |
| 200 | 400+400×0.15 |
| 300 | 600+600×0.15 |
| 400 | 800+800×0.15 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 1300多年前,我国隋朝建造的赵州石拱桥(如图)的桥拱是圆弧形,它的跨度(是弦的长)为37.4m,拱高(弧的中点到弦的距离,也叫弓形高)为7.2m,求桥拱的半径.(精确到0.1m)
1300多年前,我国隋朝建造的赵州石拱桥(如图)的桥拱是圆弧形,它的跨度(是弦的长)为37.4m,拱高(弧的中点到弦的距离,也叫弓形高)为7.2m,求桥拱的半径.(精确到0.1m)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
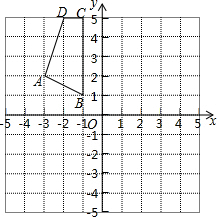 四边形ABCD在平面直角坐标系中的位置如图所示.
四边形ABCD在平面直角坐标系中的位置如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{1}{10}$ | C. | $\frac{1}{100}$ | D. | $\frac{1}{1000}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com