
分析 (1)首先转化为乘法,然后进行约分;
(2)首先把分母和分子分解因式,然后进行约分即可;
(3)利用同分母的分式的加减法进行计算即可;
(4)首先把分母和分子分解因式,计算括号内的式子,然后转化为乘法,进行乘法运算.
解答 解:(1)原式=$\frac{3c}{16a}$•$\frac{2{a}^{2}}{bc}$=$\frac{3a}{6b}$;
(2)原式=$\frac{(x+y)^{2}}{x(x-y)}$•$\frac{(x-y)^{2}}{x(x+y)}$=$\frac{(x+y)(x-y)}{{x}^{2}}$;
(3)原式=$\frac{x+2y}{{x}^{2}-{y}^{2}}$+$\frac{-y}{{x}^{2}-{y}^{2}}$-$\frac{2x}{{x}^{2}-{y}^{2}}$=$\frac{x+2y-y-2x}{(x+y)(x-y)}$=$\frac{y-x}{(x+y)(x-y)}$=-$\frac{1}{x+y}$;
(4)原式=$\frac{(a-b)(a+b)}{a-b}$÷$\frac{(a+b)^{2}}{ab}$=(a+b)•$\frac{ab}{(a+{b)}^{2}}$=$\frac{ab}{a+b}$.
点评 本题主要考查分式的混合运算,通分、因式分解和约分是解答的关键.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:解答题
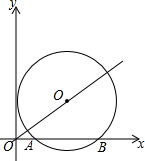 在平面直角坐标系中,⊙O′与x轴相交于A(2,0),B(8,0),⊙O′的圆心O′在直线y=$\frac{4}{5}$x上,求⊙O′的半径,并判断⊙O′与y轴的位置关系.
在平面直角坐标系中,⊙O′与x轴相交于A(2,0),B(8,0),⊙O′的圆心O′在直线y=$\frac{4}{5}$x上,求⊙O′的半径,并判断⊙O′与y轴的位置关系.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.5m | B. | 0.7m | C. | 1.6m | D. | 0.8m |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1<y2<y3 | B. | y2<y1<y3 | C. | y3<y1<y2 | D. | y1<y3<y2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com