
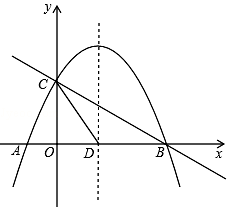
 如图,直线y=-$\frac{1}{2}$x+2与x轴交于点B,与y轴交于点C,已知二次函数的图象经过点B、C和点A(-1,0).
如图,直线y=-$\frac{1}{2}$x+2与x轴交于点B,与y轴交于点C,已知二次函数的图象经过点B、C和点A(-1,0).分析 (1)先求得B、C的坐标,然后设抛物线的解析式为y=a(x+1)(x-4),将点C的坐标代入求解即可;
(2)如图1所示:先求得抛物线的对称轴方程则可得到OD的长,然后依据勾股定理可求得CD的长,然后可求得点P和点P′的坐标,然后过点C作CE⊥对称轴,垂足为E,然后依据等腰三角形的性质可得到DE=OC=2,故此可得到点P″的坐标;
(3)设点F(a,-$\frac{1}{2}$a2+$\frac{3}{2}$a+2),则E(a,-$\frac{1}{2}$a+2),则FE=-$\frac{1}{2}$a2+2a,然后可得到△CBF的面积与a的函数关系式,从而可得到△CBF的最大值,从而可确定出点E的坐标,最后依据四边形CDBF的最大面积=△CBD的面积+△BCF的最大面积求解即可.
解答 解:(1)令直线y=-$\frac{1}{2}$x+2中,y=0得:-$\frac{1}{2}$x+2=0,解得x=4,
∴B(4,0).
令x=0得:y=2,
∴C(0,2).
设抛物线的解析式为y=a(x+1)(x-4),将点C的坐标代入得:-4a=2,解得:a=-$\frac{1}{2}$,
∴抛物线的解析式为y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2.
(2)如图2所示: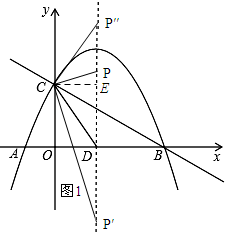
抛物线的对称轴为x=-$\frac{b}{2a}$=$\frac{3}{2}$,
∴OD=$\frac{3}{2}$.
又∵OC=2,
∴DC=$\sqrt{{2}^{2}+(\frac{3}{2})^{2}}$=$\frac{5}{2}$.
当PD=DC时,P($\frac{3}{2}$,$\frac{5}{2}$).
当P′D=CD时,P′($\frac{3}{2}$,-$\frac{5}{2}$).
过点C作CE⊥对称轴,垂足为E.
又∵CP″=CD,
∴CE=EP″.
∵DE=CO=2,
∴DP″=4.
∴P″($\frac{3}{2}$,4).
∴点P的坐标为P($\frac{3}{2}$,$\frac{5}{2}$)或P′($\frac{3}{2}$,-$\frac{5}{2}$)或P″($\frac{3}{2}$,4).
(3)如图2所示.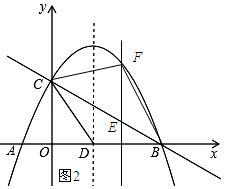
∵△CBD的面积为定值,
∴△CBF的面积最大时,四边形的面积最大.
设点F(a,-$\frac{1}{2}$a2+$\frac{3}{2}$a+2),则E(a,-$\frac{1}{2}$a+2),则FE=-$\frac{1}{2}$a2+$\frac{3}{2}$a+2-(-$\frac{1}{2}$a+2)=-$\frac{1}{2}$a2+2a.
∴△CBF的面积=$\frac{1}{2}$OB•EF=-a2+4a=-(a-2)2+4.
∴E(2,1),△CBF的最大面积为4.
∴四边形CDBF的最大面积=△CBD的面积+△BCF的面积=$\frac{1}{2}$BD•OC+4=6.5.
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求二次函数的解析式、等腰三角形的性质、二次函数的性质,依据题意列出△CBF的面积与a的函数关系是解答本题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,平面直角坐标系中,已知点A(-3,3),B(-5,1),C(-2,0),将△ABC向左平移2个单位,向下平移3个单位过后得到△A1B1C1
如图,平面直角坐标系中,已知点A(-3,3),B(-5,1),C(-2,0),将△ABC向左平移2个单位,向下平移3个单位过后得到△A1B1C1查看答案和解析>>
科目:初中数学 来源: 题型:选择题
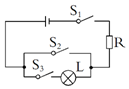 在物理课上,某实验的电路图如图所示,其中S1,S2,S3表示电路的开关,L表示小灯泡,R为保护电阻.若闭合开关S1,S2,S3中的任意两个,则小灯泡L发光的概率( )
在物理课上,某实验的电路图如图所示,其中S1,S2,S3表示电路的开关,L表示小灯泡,R为保护电阻.若闭合开关S1,S2,S3中的任意两个,则小灯泡L发光的概率( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com