Question

5．点M是直线y=2x+3上的动点，过点M作MN⊥x轴于点N，当点M位于第二象限时，在y轴上有一点P，使△MNP为等腰直角三角形，则点P的坐标为（0，1）、（0，0）、（0，$\frac{3}{4}$）．

Answer 1

分析 首先根据题意，判断出△MNP为等腰直角三角形的三种情况：（1）两条直角边是MN、MP；（2）两条直角边是MN、NP；（3）两条直角边是MP、NP；然后分类讨论，根据等腰直角三角形的两条直角边相等，以及M是直线y=2x+3上的动点，分别求出点P的坐标各是多少即可．

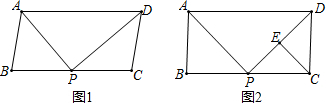
解答 解：（1）如图1，当等腰直角三角形的两条直角边是MN、MP时，，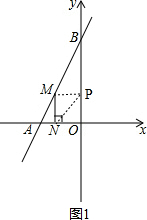
设点P的坐标为（0，a），
则点M的坐标为（-a，a），
因为点M是直线y=2x+3上的动点，
所以a=2×（-a）+3，
解得a=1，
所以点P的坐标为（0，1）；

（2）如图2，当等腰直角三角形的两条直角边是MN、NP时，，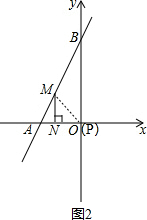
点P的坐标为（0，0），
则点M的坐标为（-b，b），
因为点M是直线y=2x+3上的动点，
所以b=2×（-b）+3，
解得b=1，
即点M的坐标为（-1，1），点N的坐标为（-1，0），点P的坐标为（0，0）；

（3）如图3，当等腰直角三角形的两条直角边是MP、NP时，，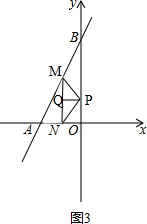
作PQ⊥MN交MN与点Q，
设点P的坐标为（0，c），
因为MP=NP，∠MPN=90°，
所以点M的坐标为（-c，2c），
因为点M是直线y=2x+3上的动点，
所以2c=2×（-c）+3，
解得a=$\frac{3}{4}$，
所以点P的坐标为（0，$\frac{3}{4}$）；
综上，可得
点P的坐标为（0，1）、（0，0）、（0，$\frac{3}{4}$）．
故答案为：（0，1）、（0，0）、（0，$\frac{3}{4}$）．

点评 （1）此题主要考查了一次函数综合题，考查了分析推理能力，考查了分类讨论思想的应用，考查了从已知函数图象中获取信息，并能利用获取的信息解答相应的问题的能力；解答此题的关键是判断出△MNP为等腰直角三角形的三种情况：（1）两条直角边是MN、MP；（2）两条直角边是MN、NP；（3）两条直角边是MP、NP．
（2）此题还考查了等腰直角三角形的性质，要熟练掌握．