
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象的顶点在第一象限,且过点(0,1)和(﹣1,0),下列结论:①ab<0,②b2>4,③0<a+b+c<2,④0<b<1,⑤当x>﹣1时,y>0.其中正确结论是___________.
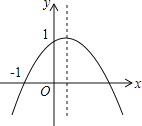
【答案】①③④
【解析】由抛物线的对称轴在y轴右侧,可以判定a、b异号,由此确定①正确;由抛物线与x轴有两个交点得到b2-4ac>0,又抛物线过点(0,1),得出c=1,由此判定②错误;由抛物线过点(-1,0),得出a-b+c=0,即a=b-1,由a<0得出b<1;由a<0,及ab<0,得出b>0,由此判定④正确;由a-b+c=0,及b>0得出a+b+c=2b>0;由b<1,c=1,a<0,得出a+b+c<a+1+1<2,由此判定③正确;由图象可知,当自变量x的取值范围在一元二次方程ax2+bx+c=0的两个根之间时,函数值y>0,由此判定⑤错误.
∵二次函数y=ax2+bx+c(a≠0)过点(0,1)和(-1,0), ∴c=1,a-b+c=0.
①∵抛物线的对称轴在y轴右侧,∴x=-![]() >0, ∴a与b异号,∴ab<0,正确;
>0, ∴a与b异号,∴ab<0,正确;
②∵抛物线与x轴有两个不同的交点,∴b2-4ac>0, ∵c=1,∴b2-4a>0,b2>4a,错误;
④∵抛物线开口向下,∴a<0,∵ab<0,∴b>0.∵a-b+c=0,c=1,∴a=b-1,
∵a<0,∴b-1<0,b<1,∴0<b<1,正确;
③∵a-b+c=0,∴a+c=b,∴a+b+c=2b>0.∵b<1,c=1,a<0,
∴a+b+c=a+b+1<a+1+1=a+2<0+2=2, ∴0<a+b+c<2,正确;
⑤抛物线y=ax2+bx+c与x轴的一个交点为(-1,0),设另一个交点为(x0,0),则x0>0,
由图可知,当x0>x>-1时,y>0,错误; 综上所述,正确的结论有①③④.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
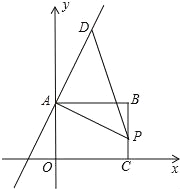
【题目】如图,矩形ABC0位于直角坐标平面,O为原点,A、C分别在坐标轴上,B的坐标为(8,6),线段BC上有一动点P,已知点D在第一象限.
(1)D是直线y=2x+6上一点,若△APD是等腰直角三角形,求点D的坐标;
(2)D是直线y=2x﹣6上一点,若△APD是等腰直角三角形.求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=5cm,BC=2cm,M,N两点分别从A,B两点以2cm/s和1cm/s的速度在矩形ABCD边上沿逆时针方向运动,其中有一点运动到点D即停止,当运动时间为_____秒时,△MBN为等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一个四边形的一条对角线把四边形分成两个等腰三角形,我们把这条对角线叫这个四边形的和谐线,这个四边形叫做和谐四边形.如菱形就是和谐四边形.

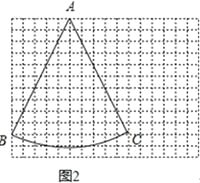
(1)如图1,在梯形ABCD中,AD∥BC,∠BAD=120°,∠C=75°,BD平分∠ABC.求证:BD是梯形ABCD的和谐线;
(2)如图2,在12×16的网格图上(每个小正方形的边长为1)有一个扇形BAC,点A.B.C均在格点上,请在答题卷给出的两个网格图上各找一个点D,使得以A、B、C、D为顶点的四边形的两条对角线都是和谐线,并画出相应的和谐四边形;
(3)四边形ABCD中,AB=AD=BC,∠BAD=90°,AC是四边形ABCD的和谐线,求∠BCD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
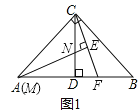
【题目】如图:已知△ABC中,CA=CB,CD⊥AB于D点,点M为线段AC上一动点,线段MN交DC于点N,且∠BAC=2∠CMN,过点C作CE⊥MN交MN延长线于点E,交线段AB于点F,探索![]() 的值.
的值.
(1)若∠ACB=90°,点M与点A重合(如图1)时:①线段CE与EF之间的数量关系是 ;②![]() = ;
= ;
(2)在(1)的条件下,若点M不与点A重合(如图2),请猜想写出![]() 的值,并证明你的猜想
的值,并证明你的猜想
(3)若∠ACB≠90°,∠CAB=![]() ,其他条件不变,请直接写出
,其他条件不变,请直接写出![]() 的值(用含有
的值(用含有![]() 的式子表示)
的式子表示)
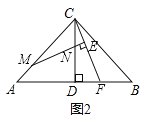
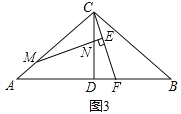
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,我国两艘海监船 A,B 在南海海域巡逻,某一时刻,两船同时收到指令,立即前往救援遇险抛锚的渔船 C,此时,B 船在A 船的正南方向 15 海里处,A 船测得渔船 C 在其南偏东 45°方向,B 船测得渔船 C 在其南偏东 53°方向,已知 A 船的航速为 30 海里/小时,B 船的航速为 25 海里/小时,问 C 船至少要等待多长时间才能得到救援?(参考数据:sin53°≈![]() ,cos53°≈
,cos53°≈![]() ,tan53°≈ 4 ,
,tan53°≈ 4 ,![]() 1.41 )
1.41 )
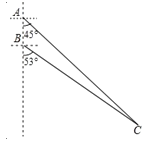
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a、b、c是常数,且a≠0)中的x与y的部分对应值如下表所示,则下列结论中,正确的个数有( )
x | -7 | -6 | -5 | -4 | -3 | -2 |
y | -27 | -13 | -3 | 3 | 5 | 3 |
①当x<-4时,y<3②当x=1时,y的值为-13;③-2是方程ax2+(b-2)x+c-7=0的一个根;④方程ax2+bx+c=6有两个不相等的实数根.
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com