
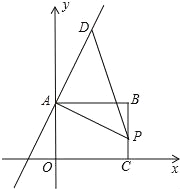
【题目】如图,矩形ABC0位于直角坐标平面,O为原点,A、C分别在坐标轴上,B的坐标为(8,6),线段BC上有一动点P,已知点D在第一象限.
(1)D是直线y=2x+6上一点,若△APD是等腰直角三角形,求点D的坐标;
(2)D是直线y=2x﹣6上一点,若△APD是等腰直角三角形.求点D的坐标.
【答案】(1)D(4,14);(2)(4,2)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
(1)根据题意可知AD=AP,作辅助线,证明△ADE≌△PAF(AAS),求得OE,代入函数解析式即可求得D坐标,
(2)分三种情况:当∠ADP=90°时,D在AB上方和下方,当∠APD=90°时.设PC=m,分别表示出D点坐标,代入y=2x﹣6,即可解题,
解;(1)如图1所示,作DE⊥y轴于E点,作PF⊥y轴于F点,可得∠DEA=∠AFP=90°,
根据题意可知当△APD为等腰直角三角形时,只有∠DAP=90°满足条件,
∴AD=AP,∠DAP=90°,
∴∠EAD+∠DAB=90°,∠DAB+∠BAP=90°,
∴∠EAD=∠BAP,
∵AB∥PF,
∴∠BAP=∠FPA,
∴∠EAD=∠FPA,
在△ADE和△PAF中,
 ,
,
∴△ADE≌△PAF(AAS),
∴AE=PF=8,OE=OA+AE=14,
设点D的横坐标为x,由14=2x+6,得x=4,
∴点D的坐标是(4,14);

(2)由点D在直线y=2x﹣6上,可设PC=m,
如图2所示,当∠ADP=90°时,AD=PD,易得D点坐标(4,2);

如图3所示,当∠APD=90°时,AP=PD,设点P的坐标为(8,m),
则D点坐标为(14﹣m,m+8),由m+8=2(14﹣m)﹣6,得m=![]() ,
,
∴D点坐标(![]() ,
,![]() );
);
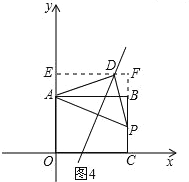
如图4所示,当∠ADP=90°时,AD=PD时,
同理可求得D点坐标(![]() ,
,![]() ),
),
D点坐标分别为(4,2)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
【题目】在一条不完整的数轴上从左到右有点A,B,C,其中点A到点B的距离为2,点C到点B的距离为8,如图所示:设点A,B,C所对应的数的和是m.
(1)若以B为原点,则点C所对应的数是 ;若以C为原点,则m的值是 .
(2)若原点O在图中数轴上,且点C到原点O的距离为4,求m的值.
(3)动点P从A点出发,以每秒3个单位长度的速度向终点C移动,动点Q同时从B点出发,以每秒2个单位的速度向终点C移动,运动时间为t秒,求P、Q两点间的距离?(用含t的代数式表示)
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
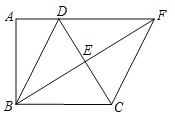
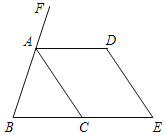
【题目】如图,四边形ABCD中,AD∥BC,∠A=90°,BD=BC,点E为CD的中点,射线BE交AD的延长线于点F,连接CF.
(1)求证:四边形BCFD是菱形;
(2)若AD=1,BC=2,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
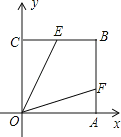
【题目】如图,在正方形OABC中,点B的坐标是(4,4),点E、F分别在边BC、BA上,OE=2![]() .若∠EOF=45°,则F点的纵坐标是( )
.若∠EOF=45°,则F点的纵坐标是( )
A.1B.![]() C.
C.![]() D.
D.![]() ﹣1
﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在下列解答中,填写适当的理由或数学式:
(1)∵AD∥BE,(已知)
∴∠B=∠. ( )
(2)∵∠E+∠ =180°,(已知)
∴AC∥DE. ( )
(3)∵ ∥ ,(已知)
∴∠ACB=∠DAC. ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
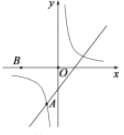
【题目】如图,反比例函数![]() 与一次函数
与一次函数![]() 在第三象限交于点
在第三象限交于点![]() .点
.点![]() 的坐标为(一3,0),点
的坐标为(一3,0),点![]() 是
是![]() 轴左侧的一点.若以
轴左侧的一点.若以![]() 为顶点的四边形为平行四边形.则点
为顶点的四边形为平行四边形.则点![]() 的坐标为_____________.
的坐标为_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,直线CD与⊙O相切于点C,且与AB的延长线交于点E.点C是弧BF的中点.
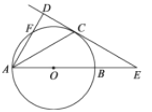
(1)求证:AD⊥CD;
(2)若∠CAD=30°.⊙O的半径为3,一只蚂蚁从点B出发,沿着BE--EC--弧CB爬回至点B,求蚂蚁爬过的路程(π≈3.14,![]() ≈1.73,结果保留一位小数.)
≈1.73,结果保留一位小数.)
查看答案和解析>>
科目:初中数学 来源: 题型:
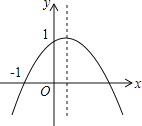
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象的顶点在第一象限,且过点(0,1)和(﹣1,0),下列结论:①ab<0,②b2>4,③0<a+b+c<2,④0<b<1,⑤当x>﹣1时,y>0.其中正确结论是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算.
(1)(﹣3)×(+4)﹣48÷|﹣6|
(2)77°53'26″+33.3°(结果用度分秒形式表示)
(3)[﹣14﹣(1﹣0.5×![]() )]×[3﹣(﹣3)2]
)]×[3﹣(﹣3)2]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com