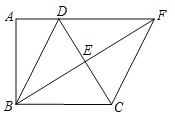
【题目】如图，四边形ABCD中，AD∥BC，∠A=90°，BD=BC，点E为CD的中点，射线BE交AD的延长线于点F，连接CF．
（1）求证：四边形BCFD是菱形；
（2）若AD=1，BC=2，求BF的长．
名校课堂系列答案科目：初中数学 来源： 题型：
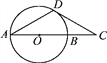
【题目】如图所示，D是半径为R的⊙O上一点，过点D作⊙O的切线交直径AB的延长线于点C，下列四个条件：①AD＝CD；②∠A＝30°；③∠ADC＝120°；④DC＝
R.其中能使得BC＝R的有________(填序号)．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】一个四位数，记千位上和百位上的数字之和为
，十位上和个位上的数字之和为
，如果
，那么称这个四位数为“和平数”．
例如：1423，
，
，因为，所以1423是“和平数”．
（1）直接写出：最小的“和平数”是 ，最大的“和平数”是 ；
（2）将一个“和平数”的个位上与十位上的数字交换位置，同时，将百位上与千位上的数字交换位置，称交换前后的这两个“和平数”为一组“相关和平数”．
例如：1423与4132为一组“相关和平数”
求证：任意的一组“相关和平数”之和是1111的倍数．
（3）求个位上的数字是千位上的数字的两倍且百位上的数字与十位上的数字之和是12的倍数的所有“和平数”；
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知在⊙O中，AB= 4
，AC是⊙O的直径，AC⊥BD于F，∠A=30°．
⑴求图中阴影部分的面积；
⑵若用阴影扇形OBD围成一个圆锥侧面，请求出这个圆锥底面圆的半径．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为提高节水意识，小申随机统计了自己家7天的用水量，并分析了第3天的用水情况，将得到的数据进行整理后，绘制成如图所示的统计图．（单位：升）
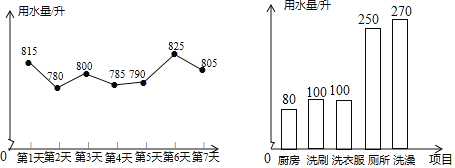
（1）求这7天内小申家每天用水量的平均数和中位数；
（2）求第3天小申家洗衣服的水占这一天总用水量的百分比；
（3）若规定居民生活用水收费标准为2.80元/立方米，请你估算小申家一个月（按30天计算）的水费是多少元？（1立方米＝1000升）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列命题正确的有（ ）
①如果等腰三角形的底角为15°，那么腰上的高是腰长的一半；
②三角形至少有一个内角不大于60°；
③连结任意四边形各边中点形成的新四边形是平行四边形；
④十边形内角和为1800°．
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目：初中数学 来源： 题型：
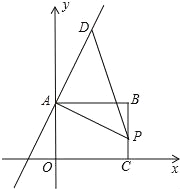
【题目】如图，矩形ABC0位于直角坐标平面，O为原点，A、C分别在坐标轴上，B的坐标为（8，6），线段BC上有一动点P，已知点D在第一象限．
（1）D是直线y＝2x+6上一点，若△APD是等腰直角三角形，求点D的坐标；
（2）D是直线y＝2x﹣6上一点，若△APD是等腰直角三角形．求点D的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
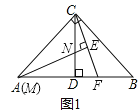
【题目】如图：已知△ABC中，CA=CB，CD⊥AB于D点，点M为线段AC上一动点，线段MN交DC于点N，且∠BAC=2∠CMN，过点C作CE⊥MN交MN延长线于点E，交线段AB于点F，探索
的值.
（1）若∠ACB=90°，点M与点A重合（如图1）时：①线段CE与EF之间的数量关系是 ；②= ；
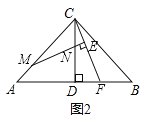
（2）在（1）的条件下，若点M不与点A重合（如图2），请猜想写出的值，并证明你的猜想
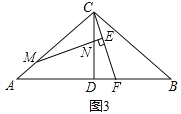
（3）若∠ACB≠90°，∠CAB=
，其他条件不变，请直接写出的值（用含有的式子表示）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
