
����Ŀ����ͼ����֪��ABC�У�CA=CB��CD��AB��D�㣬��MΪ�߶�AC��һ���㣬�߶�MN��DC�ڵ�N���ҡ�BAC=2��CMN������C��CE��MN��MN�ӳ����ڵ�E�����߶�AB�ڵ�F��̽��![]() ��ֵ.
��ֵ.
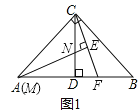
��1������ACB=90�㣬��M���A�غϣ���ͼ1��ʱ�����߶�CE��EF֮���������ϵ�� ����![]() = ��
= ��
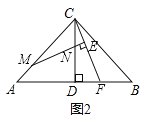
��2���ڣ�1���������£�����M�����A�غϣ���ͼ2���������д��![]() ��ֵ����֤����IJ���
��ֵ����֤����IJ���
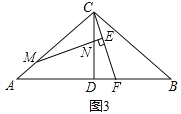
��3������ACB��90�㣬��CAB=![]() �������������䣬��ֱ��д��
�������������䣬��ֱ��д��![]() ��ֵ���ú���
��ֵ���ú���![]() ��ʽ�ӱ�ʾ��
��ʽ�ӱ�ʾ��
���𰸡���1����CE=EF���� ![]() ����2��
����2��![]() =
=![]() �����ɼ���������3��
�����ɼ���������3��![]() =
=![]() .
.
��������(1)�����ݵ��������ε����ߺ�һ�����ó���EΪCF���е㣬�Ӷ��ó��𰸣�(2)������M��MQ//AB��CD�ڵ�P����CF�ڵ�Q�����ݵ��������Ρ�ֱ�������ε����ʵó���MPN����CPQȫ�ȣ��Ӷ��ó�CE=EQ ��MC=MQ����CE=![]() CQ=
CQ=![]() MN��(3)����ͼ3��ͬ(1)��(2)�ɵ�CE=
MN��(3)����ͼ3��ͬ(1)��(2)�ɵ�CE= ![]() CQ����֤��MPN~��CPQ������
CQ����֤��MPN~��CPQ������![]() ����
����![]() ��
��
(1)����CE=EF���� ![]() ��
��
(2)��![]() =
=![]()
�������£���ͼ2��ʾ������M��MQ//AB��CD�ڵ�P����CF�ڵ�Q��
���С�CMP=��BAC=45�㣬 ��CP=MP��
�ߡ�BAC=2��CMN�� ���CMP=2��CMN�� ���CMN=��NMP=22.5�㣬��CE��MN��
���CEM=��QEM=90�㣬��CE=EQ �����ߺ�һ������CD��AB�� MQ//AB��
��CD��MQ�����MPN=��CPQ=90�㣬�֡ߡ�NCE+��CNE=��NCE+��CQN=90�㣬
���CQN=��CNE=��MNP����CP=MP�����MPN![]() ��CPQ����CE=EQ ��MC=MQ��
��CPQ����CE=EQ ��MC=MQ��
��CE=![]() CQ=
CQ=![]() MN����
MN����![]() =
=![]() ��
��
(3)��![]() =
=![]() ��
��
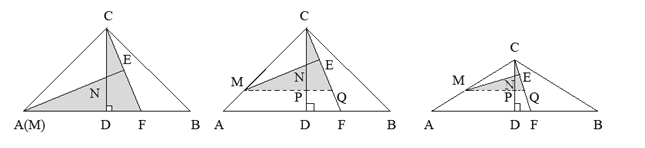
ͼ1 ͼ2 ͼ3


 ������ÿ�ʱ��ҵϵ�д�
������ÿ�ʱ��ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
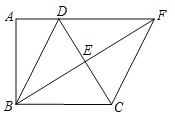
����Ŀ����ͼ���ı���ABCD�У�AD��BC����A=90�㣬BD=BC����EΪCD���е㣬����BE��AD���ӳ����ڵ�F������CF��
��1����֤���ı���BCFD�����Σ�
��2����AD=1��BC=2����BF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ����ֱ��CD���O�����ڵ�C������AB���ӳ��߽��ڵ�E����C�ǻ�BF���е㣮
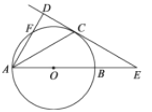
��1����֤��AD��CD��
��2������CAD=30������O�İ뾶Ϊ3��һֻ���ϴӵ�B����������BE--EC--��CB��������B��������������·��(�С�3.14��![]() ��1.73���������һλС����)
��1.73���������һλС����)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
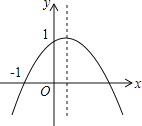
����Ŀ����ͼ�����κ���y=ax2+bx+c��a��0����ͼ��Ķ����ڵ�һ���ޣ��ҹ��㣨0��1���ͣ���1��0�������н��ۣ���ab��0����b2��4����0��a+b+c��2����0��b��1������x����1ʱ��y��0��������ȷ������___________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ͼ�ζ��������Ϊ1�������ΰ�һ���Ĺ�����ɣ����У�ͼ1�����Ϊ1����������9����ͼ2�����Ϊ1����������14����![]() �����˹��ɣ�ͼ12�����Ϊ1�������εĸ���Ϊ
�����˹��ɣ�ͼ12�����Ϊ1�������εĸ���Ϊ![]() ����
����![]()

A.64B.60C.54D.50
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ͯ������Ʊ�۸�涨���±���
��Ʊ���� | 1~50�� | 51~100�� | 100������ |
ÿ��Ʊ�ļ۸� | 13Ԫ | 11Ԫ | 9Ԫ |
ijУ���꼶��1������2�������102�˽���6��1��ͯ��ȥ�θ����������У�1�����������٣�����50�ˣ������㣬����������Ϊ��λ��Ʊ����һ��Ӧ��1218Ԫ���ʣ�
��1����������ж���ѧ����
��2���������������������Ϊһ�����幺Ʊ�����Խ�ʡ����Ǯ��
��3��������꼶��1������10��ѧ����ѧУ�������ܲμ�������Σ�����Ϊ��������Ƴ�������Ʊ�ķ�������ָ����ʡǮ�ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�����ϵ�A��ʾ����Ϊ��6����B��������A���Ҳ࣬��AB��14������M�ӵ�A��������ÿ��5����λ���ȵ��ٶ����������������˶������˶�ʱ��Ϊt��t��0���룮
![]()
��1��д�������ϵ�B��ʾ������ ������M��ʾ������ �����ú�t��ʽ�ӱ�ʾ����
��2������N�ӵ�B��������ÿ��3����λ���ȵ��ٶ����������������˶�������M��Nͬʱ�������ʵ�M�˶�������ʱ�ϵ�N��
��3����PΪAM���е㣬FΪMB���е㣬��M���˶������У��߶�PF�ij����Ƿ����仯�����仯����˵�����ɣ������䣬������߶�PF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㣮
��1������3������+4����48��|��6|
��2��77��53'26��+33��3�㣨����öȷ�����ʽ��ʾ��
��3��[��14����1��0��5��![]() ��]��[3������3��2]
��]��[3������3��2]
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ż���ְ����������棬���ǻ����ĸ����ξ���ûȥ���ֱ��������Զ��ı���ٸ�ͻ�ɽ������������Ǭ��ͷ����¡����ڽ�ʣ�����ʱ�䣬�Ż������������з羰�������ǰְ����Ż����������ξ���ͼƬ����С����״������ͼ����ȫ��ͬ���г�ǩȷ��.�ְֽ�������ͼƬ���泯��ϴ�Ⱥ����Ż��������ȡһ�ţ����Żأ����ٳ�ȡһ�ţ����鵽���������㶼�������Զ�����������������ְִ������������������Σ�����ֻ��ȥһ���������Σ�����ٸ����ɽ��Ǭ�ꡢ������������ͼƬ�ֱ���B��H��Q��F��ʾ��.
��1�����Ż��鵽�������ٸ��ͼƬ�ĸ��ʣ�
��2���������б�����״ͼ�ķ������Ż���ȥ�����������εĸ���.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com