
【题目】如图,一次函数y=kx+1(k≠0)与反比例函数![]() (m≠0)的图象有公共点A(1,2).直线l⊥x轴于点N(3,0),与一次函数和反比例函数的图象分别交于点B,C.
(m≠0)的图象有公共点A(1,2).直线l⊥x轴于点N(3,0),与一次函数和反比例函数的图象分别交于点B,C.
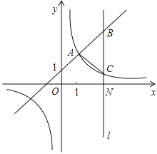
(1)求一次函数与反比例函数的解析式;
(2)求△ABC的面积?
【答案】解:(1)将A(1,2)代入一次函数解析式得:k+1=2,即k=1,∴一次函数解析式为y=x+1。
将A(1,2)代入反比例解析式得:m=2,
∴反比例解析式为![]() 。
。
(2)设一次函数与x轴交于D点,过点A作AE垂直于x轴于点E,
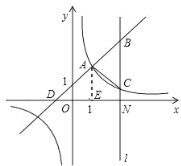
在y=x+1中,令y=0,求出x=﹣1,即OD=1。
∴A(1,2)。∴AE=2,OE=1。
∵N(3,0),∴到B横坐标为3。
将x=3代入一次函数得:y=4,
将x=3代入反比例解析式得:![]() ,
,
∴B(3,4),即ON=3,BN=4,C(3,![]() ),即CN=
),即CN=![]() ,
,
∴![]() 。
。
【解析】(1)将A坐标代入一次函数解析式中求出k的值,确定出一次函数解析式,将A坐标代入反比例函数解析式中求出m的值,即可确定出反比例解析式;
(2)设一次函数与x轴交点为D点,过A作AE垂直于x轴,由△ABC面积=△BDN面积-△ADE面积-梯形AECN面积,求出即可。


 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠BCA=90°,AC=BC,点D是BC的中点,点F在线段AD上,DF=CD,BF交CA于E点,过点A作DA的垂线交CF的延长线于点G,下列结论:①CF2=EFBF;②AG=2DC;③AE=EF;④AFEC=EFEB.其中正确的结论有( )
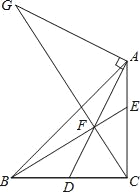
A. ①②③ B. ①②④ C. ①③④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中AC平分∠BAD,∠ADC=∠ACB=90![]() ,E为AB的中点,AC与DE交于点F.
,E为AB的中点,AC与DE交于点F.

(1)求证: ![]() =AB·AD;
=AB·AD;
(2)求证:CE//AD;
(3)若AD=6, AB=8.求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形 ABCD 的边长为 10,E 在 BC 边上运动,取 DE 的中点 G,EG 绕点 E 顺时针旋转90°得 EF,问 CE 长为多少时,A、C、F 三点在一条直线上( )
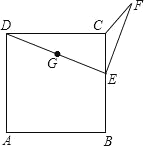
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c经过A(﹣6,0)、B(2,0)、C(0,6)三点,其顶点为D,连接AD,点P是线段AD上一个动点(不与A、D重合),过点P作y轴的垂线,垂足为点E,连接AE.
(1)求抛物线的函数解析式,并写出顶点D的坐标;
(2)如果点P的坐标为(x,y),△PAE的面积为S,求S与x之间的函数关系式,直接写出自变量x的取值范围,并求出S的最大值;
(3)过点P(﹣3,m)作x轴的垂线,垂足为点F,连接EF,把△PEF沿直线EF折叠,点P的对应点为点P,求出P的坐标.(直接写出结果)
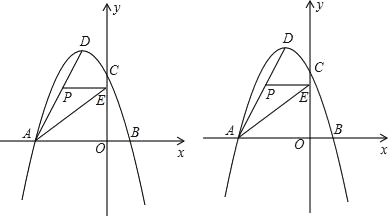
查看答案和解析>>
科目:初中数学 来源: 题型:
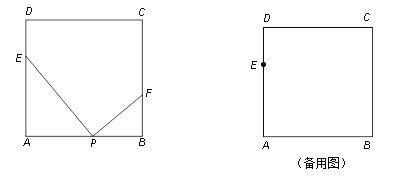
【题目】如图,在正方形ABCD中,AB=4cm,点E为AC边上一点,且AE=3cm,动点P从点A出发,以1cm/s的速度沿线段AB向终点B运动,运动时间为x s.作∠EPF=90°,与边BC相交于点F.设BF长为ycm.
(1)当x= s时,EP=PF;
(2)求在点P运动过程中,y与x之间的函数关系式;
(3)点F运动路程的长是 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知x1,x2是关于x的一元二次方程4kx2﹣4kx+k+1=0的两个实数根.
(1)是否存在实数k,使(2x1﹣x2)(x1﹣2x2)=﹣![]() 成立?若存在,求出k的值;若不存在,说明理由;
成立?若存在,求出k的值;若不存在,说明理由;
(2)求使![]() ﹣2的值为整数的实数k的整数值;
﹣2的值为整数的实数k的整数值;
(3)若k=﹣2,λ=![]() ,试求λ的值.
,试求λ的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
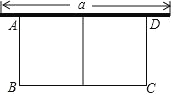
【题目】如图,有长为27m的篱笆,一面利用墙(墙的最大可用长度 a为12m),围成中间隔有一道篱笆的矩形花圃,设花圃的宽为AB=xm,面积为Sm2.
(1)求 S 与 x 的函数关系式;
(2)求矩形花圃的最大面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com