
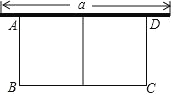
【题目】如图,有长为27m的篱笆,一面利用墙(墙的最大可用长度 a为12m),围成中间隔有一道篱笆的矩形花圃,设花圃的宽为AB=xm,面积为Sm2.
(1)求 S 与 x 的函数关系式;
(2)求矩形花圃的最大面积.
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+1(k≠0)与反比例函数![]() (m≠0)的图象有公共点A(1,2).直线l⊥x轴于点N(3,0),与一次函数和反比例函数的图象分别交于点B,C.
(m≠0)的图象有公共点A(1,2).直线l⊥x轴于点N(3,0),与一次函数和反比例函数的图象分别交于点B,C.
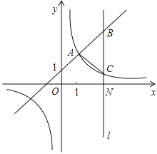
(1)求一次函数与反比例函数的解析式;
(2)求△ABC的面积?
查看答案和解析>>
科目:初中数学 来源: 题型:
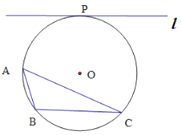
【题目】已知⊙O为△ABC的外接圆,直线l与⊙O相切于点P,且![]() ∥BC.
∥BC.
(1) 连接PO,并延长交⊙O于点D,连接AD.证明: AD平分∠BAC;
(2) 在(1)的条件下,AD交BC于点E,连接CD.若DE=2,AE=6.试求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
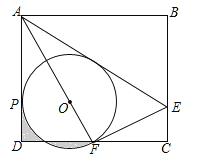
【题目】(2017四川省达州市,第16题,3分)如图,矩形ABCD中,E是BC上一点,连接AE,将矩形沿AE翻折,使点B落在CD边F处,连接AF,在AF上取点O,以O为圆心,OF长为半径作⊙O与AD相切于点P.若AB=6,BC=![]() ,则下列结论:①F是CD的中点;②⊙O的半径是2;③AE=
,则下列结论:①F是CD的中点;②⊙O的半径是2;③AE=![]() CE;④
CE;④![]() .其中正确结论的序号是__________.
.其中正确结论的序号是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线 y=x2+bx+![]() 与 y轴交于点 B,将该抛物线平移,使其经过点 A(-
与 y轴交于点 B,将该抛物线平移,使其经过点 A(-![]() ,0),且与 x轴交于另一点 C.若 b≤﹣2,则线段 OB,OC的大小关系是( )
,0),且与 x轴交于另一点 C.若 b≤﹣2,则线段 OB,OC的大小关系是( )
A. OB≤OC B. OB<OC C. OB≥OC D. OB>OC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】宾馆有50间房供游客居住,当每间房每天定价为180元时,宾馆会住满;当每间房每天的定价每增加10元时,就会空闲一间房.如果有游客居住,宾馆需对居住的每间房每天支出 20元的费用.当房价定为多少元时,宾馆当天的利润为10890元?设房价比定价 180元增加 x元,则有( )
A. (x﹣20)(50﹣![]() )=10890 B. x(50﹣
)=10890 B. x(50﹣![]() )﹣50×20=10890
)﹣50×20=10890
C. (180+x﹣20)(50﹣![]() )=10890 D. (x+180)(50﹣
)=10890 D. (x+180)(50﹣![]() )﹣50×20=10890
)﹣50×20=10890
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件20元,售价为每件25元时,每天可卖出250件.市场调查反映:如果调整价格,一件商品每涨价1元,每天要少卖出10件.
(1)求出每天所得的销售利润w(元)与每件涨价x(元)之间的函数关系式;
(2)销售单价为多少元时,该商品每天的销售利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小亮是一对双胞胎,他们的爸爸买了两套不同品牌的运动服送给他们,小明和小亮都想先挑选.于是小明设计了如下游戏来决定谁先挑选.游戏规则是:在一个不透明的袋子里装有除数字以外其它均相同的4个小球,上面分别标有数字1、2、3、4.一人先从袋中随机摸出一个小球,另一人再从袋中剩下的3个小球中随机摸出一个小球.若摸出的两个小球上的数字和为奇数,则小明先挑选;否则小亮先挑选.
(1)用树状图或列表法求出小明先挑选的概率;
(2)你认为这个游戏公平吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com