
【题目】已知抛物线 y=x2+bx+![]() 与 y轴交于点 B,将该抛物线平移,使其经过点 A(-
与 y轴交于点 B,将该抛物线平移,使其经过点 A(-![]() ,0),且与 x轴交于另一点 C.若 b≤﹣2,则线段 OB,OC的大小关系是( )
,0),且与 x轴交于另一点 C.若 b≤﹣2,则线段 OB,OC的大小关系是( )
A. OB≤OC B. OB<OC C. OB≥OC D. OB>OC
【答案】D
【解析】
由二次函数y=x2+bx![]() 的图象上点的坐标特征求得点B的坐标,由顶点坐标公式求得点A的坐标,根据抛物线平移规律和待定系数法求平移后抛物线的解析式,易比较线段OB,OC的大小关系.
的图象上点的坐标特征求得点B的坐标,由顶点坐标公式求得点A的坐标,根据抛物线平移规律和待定系数法求平移后抛物线的解析式,易比较线段OB,OC的大小关系.
如下图所示:
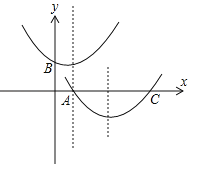
由y=x2+bx![]() (x
(x![]() )2+
)2+![]() 得到B(0,
得到B(0,![]() ),故OB
),故OB![]() .
.
该抛物线的顶点坐标是(![]() ).
).
设:抛物线向右平移了m个单位、下平移n个单位(m>0,n>0),平移后抛物线顶点坐标为(![]() m,
m,![]() ),则平移后抛物线的解析式为:y=(x
),则平移后抛物线的解析式为:y=(x![]() m)2
m)2![]() n,(xC﹣xA)2=(xC+xA)2﹣4xAxC=4n﹣b2,xC
n,(xC﹣xA)2=(xC+xA)2﹣4xAxC=4n﹣b2,xC![]() OC,OB﹣OC
OC,OB﹣OC![]() .
.
∵b≤﹣2<0,∴b+1≤﹣1<0,∴OB﹣OC![]() 0,抛物线向左平移了m个单位、下平移n个单位(m>0,n>0),用同样的方法验证:OB>OC.
0,抛物线向左平移了m个单位、下平移n个单位(m>0,n>0),用同样的方法验证:OB>OC.
故选D.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c经过A(﹣6,0)、B(2,0)、C(0,6)三点,其顶点为D,连接AD,点P是线段AD上一个动点(不与A、D重合),过点P作y轴的垂线,垂足为点E,连接AE.
(1)求抛物线的函数解析式,并写出顶点D的坐标;
(2)如果点P的坐标为(x,y),△PAE的面积为S,求S与x之间的函数关系式,直接写出自变量x的取值范围,并求出S的最大值;
(3)过点P(﹣3,m)作x轴的垂线,垂足为点F,连接EF,把△PEF沿直线EF折叠,点P的对应点为点P,求出P的坐标.(直接写出结果)
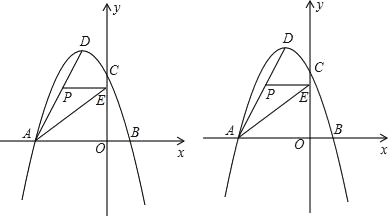
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图一次函数![]() 的图象分别交x轴、y轴于点A,B,与反比例函数
的图象分别交x轴、y轴于点A,B,与反比例函数![]() 图象在第二象限交于点C(m,6),
图象在第二象限交于点C(m,6),![]() 轴于点D,OA=OD.
轴于点D,OA=OD.
(1)求m的值和一次函数的表达式;
(2)在X轴上求点P,使△CAP为等腰三角形(求出所有符合条件的点)
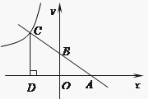
查看答案和解析>>
科目:初中数学 来源: 题型:
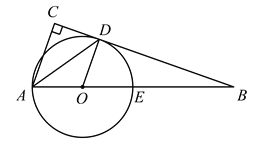
【题目】如图,在Rt△ABC中,∠ACB=90°,AD平分∠BAC交BC于点D,点O是AB边上一点,以O为圆心作⊙O且经过A,D两点,交AB于点E.
(1)求证:BC是⊙O的切线;
(2)AC=2,AB=6,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2-4x+c的图象过点(-1, 0)和点(2,-9).
(1) 求该二次函数的解析式并写出其对称轴;
(2) 已知点P(2 , -2),连结OP , 在x轴上找一点M,使△OPM是等腰三角形,请直接写出点M的坐标(不写求解过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
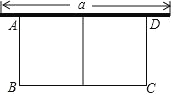
【题目】如图,有长为27m的篱笆,一面利用墙(墙的最大可用长度 a为12m),围成中间隔有一道篱笆的矩形花圃,设花圃的宽为AB=xm,面积为Sm2.
(1)求 S 与 x 的函数关系式;
(2)求矩形花圃的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
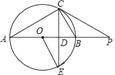
【题目】如图,已知,AB是⊙O的直径,点P在AB的延长线上,弦CE交AB于点,连结OE,AC,且∠P=∠E,∠POE=2∠CAB.
(1)求证:CE⊥AB;
(2)求证:PC是⊙O的切线;
(3)若BD=2OD,且PB=9,求⊙O的半径长和tan∠P的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.若AE=1,则FM的长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司在羊年春节晚会上举行一个游戏,规则如下:有4张背面相同的卡片,正面分别是喜羊羊、美羊羊、慢羊羊、懒羊羊的头像,分别对应1000元、600元、400元、200元的奖金,现将4张纸牌洗匀后背面朝上摆放到桌上,让员工抽取,每人有两次抽奖机会,两次抽取的奖金之和作为公司发的年终奖金.现有两种抽取的方案:①小芳抽取方案是:直接从四张牌中抽取两张.②小明抽取的方案是:先从四张牌中抽取一张后放回去,再从四张中再抽取一张.你认为是小明抽到的奖金不少于1000元的概率大还是小芳抽取到的奖金不少于1000元的概率大?请用树形图或列表法进行分析说明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com