
(本题10分)等边⊿ABC的边长为6,点E、F分别是边AC、BC上的点,连结AF,BE相交于点P.
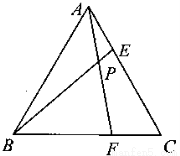
(1)若AE=CF: ①求∠APB的度数.(3分)②若AE=2,试求的 值.(3分)
值.(3分)
(2)若AF=BE,当点E从点A运动到点C时,试求点P经过的路径长.(4分)
(1)①120°;②12 ;(2) 或3
或3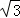 .
.
【解析】
试题分析:(1)①证明△ABE≌△CAF,借用外角即可得到答案;
②利用勾股定理求得AF的长度,再利用平行线分线段成比例定理或三角形相似的性质求得 ,即可得到答案;
,即可得到答案;
(2)当点F靠近点C的时候,点P的路径是一段弧,由题目不难看出当E为AC的中点的时候,点P经过弧AB的中点,此时△ABP为等腰三角形,继而求得半径和对应的圆心角的度数,求得答案,点F靠近点B时,点P的路径就是过点B向AC作的垂线段的长度.
试题解析:(1)①证明:∵△ABC为等边三角形,
∴AB=AC,∠C=∠CAB=60°,
在△ABE和△CAF中,
 ,
,
∴△ABE≌△CAF(SAS),
∴AF=BE,∠ABE=∠CAF.
又∵∠APE=∠BPF=∠ABP+∠BAP,
∴∠APE=∠BAP+∠CAF=60°.
∴∠APB=180°﹣∠APE=120°.
②∵∠C=∠APE=60°,∠PAE=∠CAF,
∴△APE∽△ACF,
∴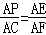 ,即
,即 ,所以APAF=12 ;
,所以APAF=12 ;
(2)若AF=BE,有AE=BF或AE=CF两种情况.
①当AE=CF时,点P的路径是一段弧,由题目不难看出当E为AC的中点的时候,点P经过弧AB的中点,此时△ABP为等腰三角形,且∠ABP=∠BAP=30°,
∴∠AOB=120°,又∵AB=6,
∴OA=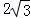 ,
,
点P的路径是 .
.
②当AE=BF时,点P的路径就是过点B向AC做的垂线段的长度;
∵等边三角形ABC的边长为6,∴点P的路径的长度为:  .
.
所以,点P经过的路径长为 或3
或3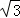 .
.

考点:等边三角形的性质;相似三角形的判定和性质;弧长公式.
考点分析: 考点1:三角形 (1)三角形的概念:由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.

 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源:2014-2015学年陕西省西安市九年级下学期第一次月考数学试卷(解析版) 题型:填空题
反比例函数 与正比例函数
与正比例函数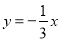 交于
交于 ,
, 两点,过点
两点,过点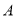 作
作 轴的平行线与过点
轴的平行线与过点 作
作 轴的平行线交于点C,则
轴的平行线交于点C,则 的面积为___________________.
的面积为___________________.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省东台市第一教研片九年级下学期第一次月考数学试卷(解析版) 题型:选择题
下列各式: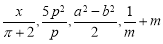 ,其中分式共有( ).
,其中分式共有( ).
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省九年级3月联考数学试卷(解析版) 题型:选择题
九(1)班6名同学某次练习一分钟跳绳的个数如下:108,120,110,124,138,140,则这组数据的中位数和极差分别为( ).
A.122,32 B.120,32 C.124,30 D.110,32
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省九年级3月联考数学试卷(解析版) 题型:解答题
(本题8分)如图1,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.
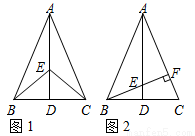
(1)求证:BE=CE;(4分)
(2)若BE的延长线交AC于点F,且BF⊥AC,垂足为F,如图2,∠BAC=45°,求证:△AEF≌△BCF.(4分)
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省泰州市高港实验学校九年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题14分)如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D.点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到C时,两点都停止.设运动时间为t秒.

(1)求线段CD的长;
(2)设△CPQ的面积为S,求S与t之间的函数关系式,并确定在运动过程中是否存在某一时刻t,使得S△CPQ:S△ABC=9:100?若存在,求出t的值;若不存在,说明理由.
(3)当t为何值时,△CPQ为等腰三角形?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com