
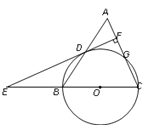
【题目】如图,等腰三角形ABC中,AC=BC=10,AB=12. 以BC为直径作⊙O交AB于点D,交AC于点G,DF⊥AC,垂足为F,交CB的延长线于点E.
(1)求证:直线EF是⊙O的切线;
(2)求sin∠E的值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)求证直线EF是⊙O的切线,只要连接OD证明OD⊥EF即可;
(2)根据∠E=∠CBG,可以把求sin∠E的值得问题转化为求sin∠CBG,进而转化为求Rt△BCG中,两边的比的问题.
(1)连结OD, CD.
∵BC是直径,
∴CD⊥AB.
∵AC=BC,
∴D是AB的中点.
又O为BC中点,
∴OD∥AC.
∵DF⊥AC,
∴OD⊥EF.
∴直线EF是⊙O的切线.
(2)连结BG.
∵BC是直径,
∴∠BGC=90°.
在Rt△BCD中, CD=![]() .
.
∵![]() AB·CD=
AB·CD=![]() AC·BG,
AC·BG,
∴BG=![]() .
.
在Rt△BGC中, CG=![]() .
.
∵BG∥EF,
∴∠E=∠CBG.
∴sin∠E=sin∠CBG=![]() .
.


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线AB与函数y=![]() (x>0)的图象交于点A(m,2),B(2,n).过点A作AC平行于x轴交y轴于点C,在y轴负半轴上取一点D,使OD=
(x>0)的图象交于点A(m,2),B(2,n).过点A作AC平行于x轴交y轴于点C,在y轴负半轴上取一点D,使OD=![]() OC,且△ACD的面积是6,连接BC.
OC,且△ACD的面积是6,连接BC.
(1)求m,k,n的值;
(2)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=10,点D是边BC上一动点 (不与B,C重合),∠ADE=∠B=α,DE交AC于点E,且 ![]() .下列结论: ①△ADE∽△ACD;②当BD=6时,△ABD与△DCE全等;③△DCE为直角三角形时,BD为8或
.下列结论: ①△ADE∽△ACD;②当BD=6时,△ABD与△DCE全等;③△DCE为直角三角形时,BD为8或![]() ;④CD2=CECA.其中正确的结论是________(把你认为正确结论的序号都填上)
;④CD2=CECA.其中正确的结论是________(把你认为正确结论的序号都填上)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB为⊙O的直径,PC切⊙O于C交AB的延长线于点P,∠CAP=35°,那么∠CPO的度数等于( )
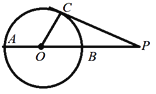
A. 15° B. 20° C. 25° D. 30°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠MAN=30°,O为边AN上一点,以点O为圆心,2为半径作⊙O,交AN于D,E两点,设AD=x.
(1)如图①,当x取何值时,⊙O与AM相切?
(2)如图②,当x为何值时,⊙O与AM相交于B,C两点,且∠BOC=90°?
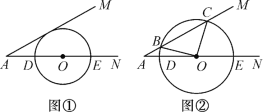
查看答案和解析>>
科目:初中数学 来源: 题型:
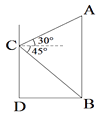
【题目】某数学兴趣小组的同学在一次活动中,为了测量某建筑物AB的高,他们来到另一建筑物CD上的点C处进行观察,如图所示,他们测得建筑物AB顶部A的仰角为30°,底部B的俯角为45°,已知建筑物AB、CD的距离DB为12m,求建筑物AB的高.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是从一副扑克牌中取出的两组牌,分别是黑桃1,2,3,4和方块1,2,3,4,将它们背面朝上分别重新洗牌后,从两组牌中各摸出一张,那么摸出的两张牌的牌面数字之和等于5的概率是多少?请你用列举法(列表或画树状图)加以分析说明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】凤城商场经销一种高档水果,售价为每千克50元
(1)连续两次降价后售价为每千克32元,若每次下降的百分率相同.求平均下降的百分率;
(2)已知这种水果的进价为每千克40元,每天可售出500千克,经市场调查发现,若每千克涨价1元,日销售量将减少20千克,每千克应涨价多少元才能使每天获得的利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线![]() 与x、y轴分别交于点A、C.抛物线的图象经过A、C和点B(1,0).
与x、y轴分别交于点A、C.抛物线的图象经过A、C和点B(1,0).

(1)求抛物线的解析式;
(2)在直线AC上方的抛物线上有一动点D,当D与直线AC的距离DE最大时,求出点D的坐标,并求出最大距离是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com