
【题目】如下图①,抛物线y=ax2+bx+3(a≠0)与x轴交于点A(![]() ,0),B(3,0),与y轴交于点C,连接BC.
,0),B(3,0),与y轴交于点C,连接BC.
(1)求抛物线的表达式;
(2)抛物线上是否存在点M,使得△MBC的面积与△OBC的面积相等,若存在,请直接写出点M的坐标;若不存在,请说明理由;
(3)点D(2,m)在第一象限的抛物线上,连接BD.在对称轴左侧的抛物线上是否存在一点P,满足∠PBC=∠DBC?如果存在,请求出点P的坐标;如果不存在,请说明理由.

【答案】(1)、y=-![]() +2x+3;(2)、M1(
+2x+3;(2)、M1(![]() ,
, ![]() ),M2(
),M2(![]() ,
, ![]() );(3)、(
);(3)、(![]() ,
, ![]() )
)
【解析】试题分析:(1)、利用待定系数法求出二次函数的解析式;(2)、根据等面积法得出点M的坐标;(3)、首先根据二次函数的解析式求出点C和点D的坐标,从而得出CD∥x轴,根据题意得出△CGB和△CDB全等,得出点G的坐标,利用待定系数法求出直线BP的函数解析式,然后求出一次函数和二次函数的交点坐标,根据点P在抛物线的左侧得出点P的坐标.
试题解析:(1)、∵抛物线![]() 与x轴交于点A(
与x轴交于点A(![]() ,0),B(3,0),
,0),B(3,0),
![]() ,解得
,解得![]() , ∴抛物线的表达式为
, ∴抛物线的表达式为![]() .
.
(2)、存在.M1(![]() ,
, ![]() ),M2(
),M2(![]() ,
, ![]() )
)
(3)、存在.如图,设BP交轴y于点G. ∵点D(2,m)在第一象限的抛物线上,
∴当x=2时,m=![]() . ∴点D的坐标为(2,3).
. ∴点D的坐标为(2,3).
把x=0代入![]() ,得y=3. ∴点C的坐标为(0,3). ∴CD∥x轴,CD = 2.
,得y=3. ∴点C的坐标为(0,3). ∴CD∥x轴,CD = 2.
∵点B(3,0),∴OB =" OC" = 3 ∴∠OBC=∠OCB=45°.
∴∠DCB=∠OBC=∠OCB=45°,又∵∠PBC=∠DBC,BC=BC,
∴△CGB ≌ △CDB(ASA),∴CG=CD=2. ∴OG=OC![]() CG=1,∴点G的坐标为(0,1).
CG=1,∴点G的坐标为(0,1).
设直线BP的解析式为y=kx+1,将B(3,0)代入,得3k+1=0,解得k=![]() .
.
∴直线BP的解析式为y=![]() x+1. 令
x+1. 令![]() x+1=
x+1=![]() .解得
.解得![]() ,
, ![]() .
.
∵点P是抛物线对称轴x=![]() =1左侧的一点,即x<1,∴x=
=1左侧的一点,即x<1,∴x=![]() .把x=
.把x=![]() 代入抛物线
代入抛物线![]() 中,解得y=
中,解得y=![]() ∴当点P的坐标为(
∴当点P的坐标为(![]() ,
, ![]() )时,满足∠PBC=∠DBC.
)时,满足∠PBC=∠DBC.
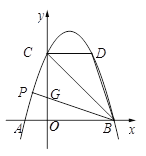


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:
【题目】已知∠AOB=90°,在∠AOB的平分线OM上有一点C,将一个三角板的直角顶点与C重合,它的两条直角边分别与OA,OB(或它们的反向延长线)相交于点D,E.
当三角板绕点C旋转到CD与OA垂直时(如图①),易证:OD+OE=![]() OC;
OC;
当三角板绕点C旋转到CD与OA不垂直时,即在图②,图③这两种情况下,上述结论是否仍然成立?若成立,请给予证明;若不成立,线段OD,OE,OC之间又有怎样的数量关系?请写出你的猜想,不需证明.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,以AC为直径作⊙O交AB于点D,E为BC的中点,连接DE并延长交AC的延长线于点F.
(1)求证:DE是⊙O的切线;
(2)若CF=2,DF=4,求⊙O直径的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,点D,E分别是边BC,AB上的中点,连接DE并延长至点F,使EF=2DF,连接CE、AF.
(1)证明:AF=CE;
(2)当∠B=30°时,试判断四边形ACEF的形状并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中有一个四边形ABCD.
(1)分别写出点A,B,C,D的坐标;
(2)求四边形ABCD的面积;
(3)将四边形ABCD先向下平移3个单位长度,再向右平移4个单位长度后得到的四边形A1B1C1D1,画出四边形A1B1C1D1

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了让孩子们了解更多的海洋文化知识,市海洋局购买了一批有关海洋文化知识的科普书籍和绘本故事书籍捐赠给市里的几所中小学校.经了解,以两类书的平均单价计算,30本科普书籍和50本绘本故事书籍共需2100元;20本科普书籍比10本绘本故事书籍多100元.
(1)求平均每本科普书籍和绘本故事书籍各是多少元.
(2)计划每所学校捐赠书籍数目和总费用相同.其中每所学校的科普书籍大于115本,科普书籍比绘本故事书籍多30本,总费用不超过5000元,请求出所有符合条件的购书方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知点A(-2,0).点D在y轴上,连接AD并将它沿x轴向右平移至BC的位置,且点B坐标为(4,0),连接CD,OD=![]() AB.
AB.
(1)线段CD的长为 ,点C的坐标为 ;
(2)如图2,若点M从点B出发,以1个单位长度/秒的速度沿着x轴向左运动,同时点N从原点O出发,以相同的速度沿折线OD→DC运动(当N到达点C时,两点均停止运动).假设运动时间为t秒.
①t为何值时,MN∥y轴;
②求t为何值时,S△BCM=2S△ADN.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com