
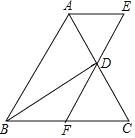
【题目】如图,△ABC 是等边三角形,D 为 AC 上一点连接 BD,旋转△BCD,使点 B 落在 BC上方的点 E 处,点 C 落在 BC 上的点 F 处,点 D 落在点 C 处,连接 AE.
求证:四边形 ABFE 是平行四边形.
科目:初中数学 来源: 题型:
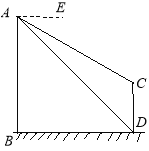
【题目】如图,AB、CD为两个建筑物,建筑物AB的高度为60米,从建筑物AB的顶点A点测得建筑物CD的顶点C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°.
(1)求两建筑物底部之间水平距离BD的长度;
(2)求建筑物CD的高度(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一组数据a,b,c的平均数为5,方差为4,那么数据a+2,b+2,c+2的平均数和方差分别是( )
A.5,4B.4,5C.7,4D.7,3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知菱形OABC在平面直角坐标系的位置如图所示,顶点A(5,0),OB=4![]() ,点P是对角线OB上的一个动点,D(0,1),当CP+DP最短时,点P的坐标为( )
,点P是对角线OB上的一个动点,D(0,1),当CP+DP最短时,点P的坐标为( )

A. (0,0) B. (1,![]() ) C. (
) C. (![]() ,
,![]() ) D. (
) D. (![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】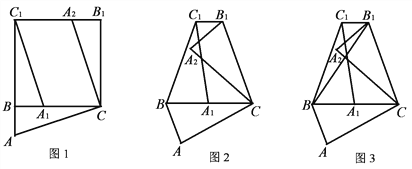
(1)如图1,在Rt△ABC中,∠ABC=90°,以点B为中心,把△ABC逆时针旋转90°,得到△A1BC1;再以点C为中心,把△ABC顺时针旋转90°,得到△A2B1C,连接C1B1,则C1B1与BC的位置关系为_______;
(2)如图2,当△ABC是锐角三角形,∠ABC=α(α≠60°)时,将△ABC按照(1)中的方式旋转α,连接C1B1,探究C1B1与BC的位置关系,写出你的探究结论,并加以证明;
(3)如图3,在图2的基础上,连接B1B,若C1B1=![]() BC,△C1BB1的面积为4,则△B1BC的面积为 .
BC,△C1BB1的面积为4,则△B1BC的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
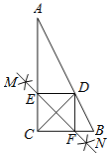
【题目】如图,Rt△ABC中,∠ACB=90°,CD平分∠ACB交AB于点D,按下列步骤作图:
步骤1:分别以点C和点D为圆心,大于![]() 的长为半径作弧,两弧相交于M,N两点;
的长为半径作弧,两弧相交于M,N两点;
步骤2:作直线MN,分别交AC,BC于点E,F;
步骤3:连接DE,DF.
若AC=4,BC=2,则线段DE的长为![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD 中,点E在AD上,EC∥AB,EB∥DC,若△ABE面积为5,△ECD的面积为1,则△BCE的面积是__________.
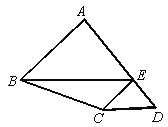
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人民生活水平的不断提高,我市家庭轿车的拥有量逐年增加.据统计,某小区2015年底拥有家庭轿车64辆,2017年底家庭轿车的拥有量达到100辆.
(1)若该小区2015年底到2018年底家庭轿车拥有量的年平均增长率都相同,求该小区到2018年底家庭轿车将达到多少辆?
(2)为了缓解停车矛盾,该小区决定投资15万元再建造若干个停车位.据测算,建造费用分别为室内车位5000元/个,露天车位1000元/个,考虑到实际因素,计划露天车位的数量不少于室内车位的2倍,但不超过室内车位的2.5倍,求该小区最多可建两种车位各多少个?试写出所有可能的方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com