Question

【题目】如图，已知在△ABC中，AD平分∠BAC，EM是AD的中垂线，交BC延长线于E．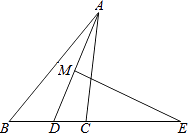
（1）连接AE，证明：∠EAC=∠B．
（2）求证：DE2=BECE．

Answer 1

【答案】
（1）证明：

∵EM是AD的中垂线，

∴EA=ED，

∴∠EAD=∠EDA，

又∵AD平分∠BAC，

∴∠CAD=∠BDA，

∵∠EAD=∠EAC+∠CAD，∠ADE=∠B+∠BAD，

∴∠EAC=∠B

（2）证明：在△EAC和△EBA中，

∠AEC=∠AEC，∠EAC=∠B，

∴△EAC∽△EBA，

∴ = ，

∴AE2=BECE，

∵DE=AE，

∴DE2=BECE

【解析】（1）根据线段垂直平分线性质求出AE=DE，求出∠EAD=∠EDA，根据角平分线定义得出∠CAD=∠BDA，即可求出答案；（2）根据相似三角形的判定得出△EAC∽△EBA，得出比例式，即可得出答案．
【考点精析】根据题目的已知条件，利用线段垂直平分线的性质和相似三角形的判定与性质的相关知识可以得到问题的答案，需要掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线；线段垂直平分线的性质定理：线段垂直平分线上的点和这条线段两个端点的距离相等；相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方．