
【题目】如图,△ABC和△BCD都是等边三角形,连接BE、AD交于O.
求证:(1)AD=BE (2)∠AOB=60°.

【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)根据等边三角形的性质可得![]()
![]() 然后求出
然后求出![]() 再利用“边角边”证明
再利用“边角边”证明![]() 和
和![]() 全等,根据全等三角形对应边相等证明即可;
全等,根据全等三角形对应边相等证明即可;
(2)根据全等三角形对应角相等可得![]() 然后求出
然后求出![]() 再根据三角形的内角和等于180°列式计算即可得解.
再根据三角形的内角和等于180°列式计算即可得解.
试题解析:证明:(1)∵△ABC和△ECD都是等边三角形,
∴AC=BC,CD=CE, ![]()
∴∠ACB+∠ACE=∠DCE+∠ACE,
即∠ACD=∠BCE,
在△ACD和△BCE中,
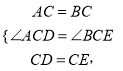
∴△ACD≌△BCE(SAS),
∴AD=BE;
(2)∵△ACD≌△BCE,
∴∠CAD=∠CBE,
∴∠OAB+∠OBA=∠BAC+∠CAD+∠ABO,
=∠BAC+∠CBE+∠ABO,
=∠BAC+∠ABC,
![]()
在△ABO中, ![]()
即![]()


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,AD平分∠BAC,EM是AD的中垂线,交BC延长线于E. 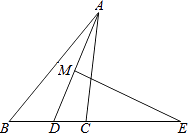
(1)连接AE,证明:∠EAC=∠B.
(2)求证:DE2=BECE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次中学生田径运动会上,根据参加男子跳高初赛的运动员的成绩(单位:m),绘制出如下的统计图①和图②,请根据相关信息,解答下列问题:

(Ⅰ)图1中a的值为 ;
(Ⅱ)求统计的这组初赛成绩数据的平均数、众数和中位数;
(Ⅲ)根据这组初赛成绩,由高到低确定9人进入复赛,请直接写出初赛成绩为1.65m的运动员能否进入复赛.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图的直角坐标系中,画出函数y=-2x+3的图象,并结合图象回答下列问题:
(1)y的值随x值的增大而 (填“增大”或“减小”);
(2)图象与x轴的交点坐标是 ;图象与y轴的交点坐标是 ;
(3)当x 时,y <0 ;
(4)直线y=-2x+3与两坐标轴所围成的三角形的面积是: .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在城镇化建设中,开发商要处理A地大量的建筑垃圾,A地只能容纳1台装卸机作业,装卸机平均每6分钟可以给工程车装满一车建筑垃圾,每辆工程车要将建筑垃圾运送至20千米的B处倾倒,每次倾倒时间约为1分钟,倾倒后立即返回A地等候下一次装运,直到装运完毕;工程车的平均速度为40千米/时.
(1)一辆工程车运送一趟建筑垃圾(从装车到返回)需要多少分钟?
(2)至少安排多少辆工程车既能保证装卸机不空闲,又能保证工程车最少等候时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某化妆品店老板到厂家选购A、B两种品牌的化妆品,若购进A品牌的化妆品5套,B品牌的化妆品6套,需要950元;若购进A品牌的化妆品3套,B品牌的化妆品2套,需要450元.
![]() 求A、B两种品牌的化妆品每套进价分别为多少元?
求A、B两种品牌的化妆品每套进价分别为多少元?
![]() 若销售1套A品牌的化妆品可获利30元,销售1套B品牌的化妆品可获利20元,根据市场需求,化妆品店老板决定,购进B品牌化妆品的数量比购进A品牌化妆品数量的2倍还多4套,且B品牌化妆品最多可购进40套,这样化妆品全部售出后,可使总的获利不少于1200元,问有几种进货方案?如何进货?
若销售1套A品牌的化妆品可获利30元,销售1套B品牌的化妆品可获利20元,根据市场需求,化妆品店老板决定,购进B品牌化妆品的数量比购进A品牌化妆品数量的2倍还多4套,且B品牌化妆品最多可购进40套,这样化妆品全部售出后,可使总的获利不少于1200元,问有几种进货方案?如何进货?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在你标有刻度的直线l上,从点A开始,以AB=1为直径画半圆,记为第1个半圆;以BC=2为直径画半圆,记为第2个半圆;以CD=4为直径画半圆,记为第3个半圆;以DE=8为直径画半圆,记为第4个半圆…,按此规律,则第4个半圆的面积是第3个半圆面积的倍,第n个半圆的面积为 . (结果保留π) 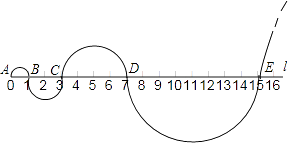
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com