
分析 (1)方程整理后,利用公式法求出解即可;
(2)分别求出不等式组中两不等式的解集,找出解集的公共部分即可.
解答 解:(1)方程整理得:x2+4x+1=0,
这里a=1,b=4,c=1,
∵△=16-4=12,
∴x=$\frac{-4±2\sqrt{3}}{2}$=-2±$\sqrt{3}$;
(2)$\left\{\begin{array}{l}{3x+4>x①}\\{5x-5<4x-2②}\end{array}\right.$,
由①得:x>-2,
由②得:x<3,
则不等式组的解集为-2<x<3.
点评 此题考查了解一元二次方程-公式法,以及解一元一次不等式组,熟练掌握运算法则是解本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
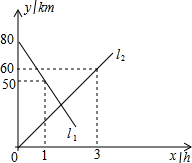 如图,A、B两地相距80km,甲、乙两人骑车分别从A、B两地同时相向而行,他们都保持匀速行驶,l1,l2分别表示甲、乙两人离B地的距离y/km与骑车时间x/h的函数关系.
如图,A、B两地相距80km,甲、乙两人骑车分别从A、B两地同时相向而行,他们都保持匀速行驶,l1,l2分别表示甲、乙两人离B地的距离y/km与骑车时间x/h的函数关系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
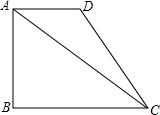 如图,在梯形ABCD中,AD∥BC,AB⊥BC,已知AD=2,cot∠ACB=$\frac{4}{3}$,梯形ABCD的面积是9;
如图,在梯形ABCD中,AD∥BC,AB⊥BC,已知AD=2,cot∠ACB=$\frac{4}{3}$,梯形ABCD的面积是9;查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-2x2)3=-6x6 | B. | (y+x)(-y+x)=y2-x2 | C. | (a3)2•a4=a9 | D. | 3$\sqrt{a}$+4$\sqrt{a}$=7$\sqrt{a}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
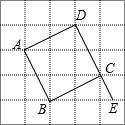 如图,在5×5的正方形网格中,每个小正方形的边长为1,四边形ABCD的每个顶点都在格点上,延长DC与过点B的水平网格线交于点E,则线段CE的长为$\frac{\sqrt{5}}{2}$.
如图,在5×5的正方形网格中,每个小正方形的边长为1,四边形ABCD的每个顶点都在格点上,延长DC与过点B的水平网格线交于点E,则线段CE的长为$\frac{\sqrt{5}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知二次函数h=x2-(2m-1)x+m2-m(m是常数,且m≠0)
已知二次函数h=x2-(2m-1)x+m2-m(m是常数,且m≠0)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在一张透明的纸上画一条直线l,在l外任取一点Q,并折出过点Q且与l垂直的直线,能折出这样的直线的条数为( )
如图,在一张透明的纸上画一条直线l,在l外任取一点Q,并折出过点Q且与l垂直的直线,能折出这样的直线的条数为( )| A. | 0条 | B. | 1条 | C. | 2条 | D. | 无数条 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com