
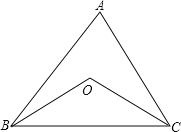
【题目】如图,在等腰△ABC中,∠A=80°,∠B和∠C的平分线相交于点O
(1)连接OA,求∠OAC的度数;
(2)求:∠BOC。
【答案】(1) 40°;(2) 130°
【解析】
试题(1)连接AO,利用等腰三角形的对称性即可求得∠OAC的度数;(2)利用三角形的内角和定理以及角平分线的定义求∠BOC与∠A的关系,再把∠A代入即可求∠BOC的度数.
试题解析:
(1)连接AO,
∵在等腰△ABC中,∠B和∠C的平分线相交于点O,
∴等腰△ABC关于线段AO所在的直线对称,
∵∠A=80°,
∴∠OAC=40°
(2)∵BO、CO分别平分∠ABC和∠ACB,
∴∠OBC= ∠ABC,∠OCB=∠ACB,
∴∠BOC=180°-(∠OBC+∠OCB)
=180°-( ∠ABC+∠ACB)
=180°- (∠ABC+∠ACB)
=180°- (180°-∠A)
=90°+∠A。
∴当∠A=80°时,
∠BOC=180° (∠B+∠C)=90°+∠A=130°。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】2018年1月20日,山西迎来了“复兴号”列车,与“和谐号”相比,“复兴号”列车时速更快,安全性更好.已知“太原南﹣北京西”全程大约500千米,“复兴号”G92次列车平均每小时比某列“和谐号”列车多行驶40千米,其行驶时间是该列“和谐号”列车行驶时间的![]() (两列车中途停留时间均除外).经查询,“复兴号”G92次列车从太原南到北京西,中途只有石家庄一站,停留10分钟.求乘坐“复兴号”G92次列车从太原南到北京西需要多长时间.
(两列车中途停留时间均除外).经查询,“复兴号”G92次列车从太原南到北京西,中途只有石家庄一站,停留10分钟.求乘坐“复兴号”G92次列车从太原南到北京西需要多长时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直立于地面上的电线杆AB,在阳光下落在水平地面和坡面上的影子分别是BC、CD,测得BC=6米,CD=4米,∠BCD=150°,在D处测得电线杆顶端A的仰角为30°,试求电线杆的高度(结果保留根号)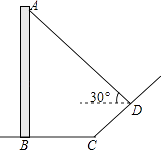
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了提升初中学生学习数学的兴趣,培养学生的创新精神,举办“玩转数学”比赛.现有甲、乙两个小组进入决赛,评委从研究报告、小组展示、答辩三个方面为各小组打分,各项成绩均按百分制记录.甲、乙两个小组各项得分如下表:
小组 | 研究报告 | 小组展示 | 答辩 |
甲 | 91 | 80 | 78 |
乙 | 79 | 83 | 90 |
(1)计算各小组的平均成绩,并从高分到低分确定小组的排名顺序;
(2)如果研究报告、小组展示、答辩按照4:3:3计算成绩,哪个小组的成绩最高?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰△ABC中,∠A=36°,∠ABC=∠ACB,∠1=∠2,∠3=∠4,BD与CE交于点O,则图中等腰三角形有( )

A. 6个 B. 7个 C. 8个 D. 9个
查看答案和解析>>
科目:初中数学 来源: 题型:
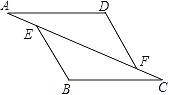
【题目】如图,已知:在△AFD和△CEB中,点A、E、F、C在同一直线上,AE=CF,∠B=∠D,AD∥BC.
(1)AD与BC相等吗?请说明理由;
(2)BE与DF平行吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,且抛物线经过A(﹣1,0),C(0,﹣5)两点,与x轴交于点B.
(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)设点P为抛物线上的一个动点,连接PB、PC,若△BPC是以BC为直角边的直角三角形,求此时点P的坐标;
(3)在抛物线上BC段有另一个动点Q,以点Q为圆心作⊙Q,使得⊙Q与直线BC相切,在运动的过程中是否存在一个最大⊙Q?若存在,请直接写出最大⊙Q的半径;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,边长为2的正方形OABC的顶点A、C分别在x轴、y轴的正半轴上,二次函数y=﹣ ![]() x2+bx+c的图象经过B、C两点.
x2+bx+c的图象经过B、C两点.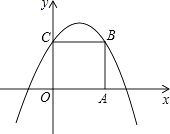
(1)求该二次函数的解析式;
(2)结合函数的图象探索:当y>0时x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线经过A(﹣1,0),B(5,0),C(0,- ![]() )三点.
)三点.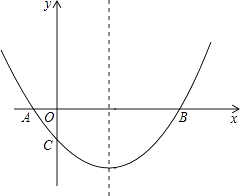
(1)求抛物线的解析式;
(2)在抛物线的对称轴上有一点P,使PA+PC的值最小,求点P的坐标;
(3)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com