
【题目】如图,在平行四边形ABCD中,BD=2AB,AC与BD相交于点O,点E、F、G分别是OC、OB、AD的中点.
求证:(1)DE⊥OC;
(2)EG=EF.

【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)由四边形ABCD是平行四边形,AC与BD相交于点O,根据平行四边形的性质,即可得BD=2OD,AB=CD,AD=BC,又由BD=2AB,可得△ODC是等腰三角形,根据三线合一的性质,即可证得DE⊥OC;
(2)由DE⊥OC,点G是AD的中点,利用直角三角形斜边上的中线等于斜边的一半,即可得EG=![]() AD,又由三角形中位线的性质,求得EF=
AD,又由三角形中位线的性质,求得EF=![]() BC,则可证得EG=EF.
BC,则可证得EG=EF.
试题解析:(1)∵四边形ABCD是平行四边形,AC与BD相交于点O,
∴BD=2OD,AB=CD,AD=BC.
∵BD=2AB,
∴OD=AB=CD.
∵点E是OC的中点,
∴DE⊥OC.
(2)∵DE⊥OC,点G是AD的中点,
∴EG=![]() AD;
AD;
∵点E、F分别是OC、OB的中点.
∴EF=![]() BC.
BC.
∵AD=BC,
∴EG=EF.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:
【题目】如图,某汽车在路面上朝正东方向匀速行驶,在A处观测到楼H在北偏东60°方向上,行驶1小时后到达B处,此时观测到楼H在北偏东30°方向上,那么该车继续行驶( )分钟可使汽车到达离楼H距离最近的位置. 
A.60
B.30
C.15
D.45
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程或方程组解应用题:
为响应市政府“绿色出行”的号召,小张上班由自驾车改为骑公共自行车.已知小张家距上班地点10千米.他用骑公共自行车的方式平均每小时行驶的路程比他用自驾车的方式平均每小时行驶的路程少45千米,他从家出发到上班地点,骑公共自行车方式所用的时间是自驾车方式所用的时间的4倍.小张用骑公共自行车方式上班平均每小时行驶多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)直角三角形有一个非常重要的性质质:直角三角形斜边上的中线等于斜边的一半,比如:如图1,Rt△ABC中,∠C=90°,D为斜边AB中点,则CD=AD=BD=-AB.请你利用该定理和以前学过的知识解决下列问题:
在△ABC中,直线![]() 绕顶点A旋转.
绕顶点A旋转.
(1)如图2,若点P为BC边的中点,点B、P在直线![]() 的异侧,BM⊥直线
的异侧,BM⊥直线![]() 于点M,CN⊥直线
于点M,CN⊥直线![]() 于点N,连接PM、PN.求证:PM=PN;
于点N,连接PM、PN.求证:PM=PN;
(2)如图3,若点B、P在直线![]() 的同侧,其它条件不变,此时PM=PN还成立吗?若成立,请给予证明;若不成立,请说明理由;
的同侧,其它条件不变,此时PM=PN还成立吗?若成立,请给予证明;若不成立,请说明理由;
(3)如图4,∠BAC=90°,直线![]() 旋转到与BC垂直的位置,E为AB上一点且AE=AC,EN⊥
旋转到与BC垂直的位置,E为AB上一点且AE=AC,EN⊥![]() 于N,连接EC,取EC中点P,连接PM、PN,求证:PM⊥PN.
于N,连接EC,取EC中点P,连接PM、PN,求证:PM⊥PN.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD的边长为2,E为BC边的延长线上一点,CE=2,联结AE,与CD交于点F,联结BF并延长与线段DE交于点G,则BG的长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在△ABC中,AB=AC=5,BC=6,AD是BC边上的中线,四边形ADBE是平行四边形.
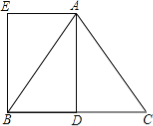
(1)求证:四边形ADBE是矩形;
(2)求矩形ADBE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电子品牌商下设台式电脑部、平板电脑部、手机部等.2018年的前五个月该品牌全部商品销售额共计600万元.下表表示该品牌商2018年前五个月的月销售额(统计信息不全).图1表示该品牌手机部各月销售额占该品牌所有商品当月销售额的百分比情况统计图.
品牌月销售额统计表(单位:万元)
月份 | 1月 | 2月 | 3月 | 4月 | 5月 |
品牌月销售额 | 180 | 90 | 115 | 95 |

(![]() )该品牌5月份的销售额是 万元;
)该品牌5月份的销售额是 万元;
(![]() )手机部5月份的销售额是 万元;
)手机部5月份的销售额是 万元;
小明同学观察图1后认为,手机部5月份的销售额比手机部4月份的销售额减少了,你同意他的看法吗?请说明理由;
(![]() )该品牌手机部有A、B、C、D、E五个机型,图2表示在5月份手机部各机型销售额占5月份手机部销售额的百分比情况统计图.则5月份 机型的销售额最高,销售额最高的机型占5月份该品牌销售额的百分比是 .
)该品牌手机部有A、B、C、D、E五个机型,图2表示在5月份手机部各机型销售额占5月份手机部销售额的百分比情况统计图.则5月份 机型的销售额最高,销售额最高的机型占5月份该品牌销售额的百分比是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列结论:
①若a+b+c=0,且abc≠0,则![]() ;
;
②若a+b+c=0,且a≠0,则x=1一定是方程ax+b+c=0的解;
③若a+b+c=0,且abc≠0,则abc>0;
④若|a|>|b|,则![]() >0.
>0.
其中正确的结论是( )
A. ①②③ B. ①②④ C. ②③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE= 度;
(2)设∠BAC=α,∠BCE=β.
①如图2,当点D在线段BC上移动,则α,β之间有怎样的数量关系?请说明理由;
②当点D在直线BC上移动,则α,β之间有怎样的数量关系?请直接写出你的结论.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com