
【题目】已知在△ABC中,AB=AC=5,BC=6,AD是BC边上的中线,四边形ADBE是平行四边形.
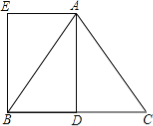
(1)求证:四边形ADBE是矩形;
(2)求矩形ADBE的面积.
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,∠BAC=90°,AB=AC,直线MN过点A且MN∥BC,点D是直线MN上一点,不与点A重合.
(1)若点E是图1中线段AB上一点,且DE=DA,请判断线段DE与DA的位置关系,并说明理由;
(2)请在下面的A,B两题中任选一题解答.
A:如图2,在(1)的条件下,连接BD,过点D作DP⊥DB交线段AC于点P,请判断线段DB与DP的数量关系,并说明理由;
B:如图3,在图1的基础上,改变点D的位置后,连接BD,过点D作DP⊥DB交线段CA的延长线于点P,请判断线段DB与DP的数量关系,并说明理由.

我选择: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线y=2x﹣2与曲线y= ![]() (x>0)相交于点A(2,n),与x轴、y轴分别交于点B,C.
(x>0)相交于点A(2,n),与x轴、y轴分别交于点B,C.
(1)求曲线的解析式;
(2)试求ABAC的值?
(3)如图2,点E是y轴正半轴上一动点,过点E作直线AC的平行线,分别交x轴于点F,交曲线于点D.是否存在一个常数k,始终满足:DEDF=k?如果存在,请求出这个常数k;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连接EF,BF;EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC,FC=2,则AB的长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,BD=2AB,AC与BD相交于点O,点E、F、G分别是OC、OB、AD的中点.
求证:(1)DE⊥OC;
(2)EG=EF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,AD平分∠BAC,AD⊥BC,垂足为D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为E.
(1)求证:四边形ADCE是矩形;
(2)当△ABC满足什么条件时,四边形ADCE是正方形?给出证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,E是CD上的一点,△ABF是△ADE的旋转图形.
(1)写成由△ADE顺时针旋转到△ABF的旋转中心、旋转角的度数.
(2)连接EF,判断并说明△AEF的形状.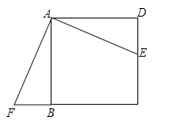
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D、E分别是AB、BC上的点,且DE∥AC,若S△BDE:S△CDE=1:4,则S△BDE:S△ACD=( )
A.1:16
B.1:18
C.1:20
D.1:24
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com