练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    20．若三角形三条边长分别是1，a，5（其中a为整数），则a的取值为5．

    分析 根据三角形三边关系：①任意两边之和大于第三边；②任意两边之差小于第三边，即可得出第三边的取值范围．

    解答 解：∵三角形的两边长分别为1和5，
    ∴第三边长x的取值范围是：5-1＜a＜5+1，
    即：4＜a＜6，
    ∴a的值为5，
    故答案为：5．

    点评 此题主要考查了三角形三边关系，熟练掌握三角形的三边关系定理是解决问题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    10．如图1，在矩形OABC中，点A的坐标为（0，-2），顶点坐标为（2，-6）的抛物线过A，B两点，设点P是∠AOC平分线上的一个动点（不与点O重合）．
    （1）求抛物线的解析式；
    （2）当点P运动到何处时，△PBC的周长最小？求此时点P的坐标和△PBC的周长；
    （3）如图2，过点P作x轴的垂线交抛物线于点Q，设∠AOC的平分线与AB交于点N，问是否存在点P，使得以P，N，Q为顶点的三角形是等腰直角三角形？若存在，请直接写出点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    11．一名射击爱好者7次射击的中靶环数如下（单位：环）：7，10，9，8，7，9，9，这7个数据的中位数是（　　）
    A．7环B．8环C．9环D．10环

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

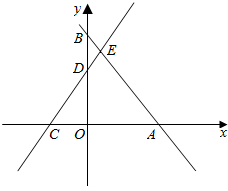    8．如图，直线AB与x轴、y轴分别交于点A，B，直线CD与x轴、y轴分别交于点C，D，AB与CD相交于点E，线段OA，OC的长是一元二次方程x2-9x+18=0的两根（OA＞OC），BE=5，tan∠ABO=$\frac{3}{4}$
    （1）求点A，C的坐标；
    （2）求AB的长；
    （3）若反比例函数y=$\frac{k}{x}$的图象经过点E，求k的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．我市嘉积镇组织20辆汽车装运完A、B、C三种荔枝共100吨到外地销售．按计划，20辆汽车都要装运，每辆汽车只能装运同一种荔枝，且必须装满．根据下表提供的信息，解答以下问题：
    荔枝  品  种ABC
    每辆汽车运载量（吨）654
    每吨荔枝获得（百元）121610
    （1）设装运A种荔枝的车辆数为x，装运B种荔枝的车辆数为y，求y与x之间的函数关系式；
    （2）若装运每种荔枝的车辆数都不少于4辆，则车辆的安排方案有几种，并写出具体方案；若要使此次销售获利最大，应采用哪种安排方案？并求出最大利润的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．解不等式 （组）：
    （1）$x-\frac{x+2}{2}≤\frac{2x-5}{3}$；    
    （2）$\left\{{\begin{array}{l}{2x+5≤3（x+2）}\\{\frac{x-1}{2}＜\frac{x}{3}}\end{array}}\right.$，并写出其整解数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

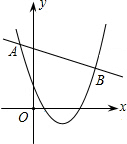    12．已知二次函数${y_1}=a{x^2}+bx+c$（a≠0）与一次函数y2=kx+m（k≠0）的图象交于点A（-2，4），B（8，2），如图所示，则能使y1＞y2成立的x的取值范围是（　　）
    A．x＜-2B．x＞8C．-2＜x＜8D．x＜-2或x＞8

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．观察下列算式：31=3，32=9，33=27，34=81，35=243，36=729，…，通过观察，用你所发现的规律确定32006的个位数字是9．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

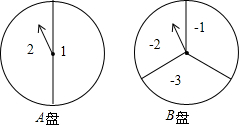    10．如图有两个可自由转动的转盘，A转盘被平均分成2个相等的扇形区域，分别标注数字1和2；B转盘被平均分成3个相等的扇形区域，分别标注数字-1，-2，-3．分别转动这两个转盘，将A盘所得结果记为x，B盘所得结果记为y，这样就确定了点P的坐标（x，y）
    （1）用列表或树状图法写出点P的所有可能性；
    （2）求点P落在直线y=2x-5上的概率．

    查看答案和解析>>

    同步练习册答案