
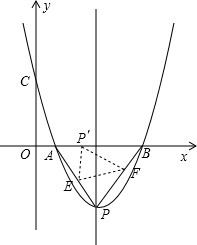
 已知:抛物线经过A(2,0)、B(8,0)、C(0,$\frac{16\sqrt{3}}{3}$);设抛物线的顶点为P,把△APB翻折,使点P落在线段AB上(不与A、B重合),记作P′,折痕为EF.
已知:抛物线经过A(2,0)、B(8,0)、C(0,$\frac{16\sqrt{3}}{3}$);设抛物线的顶点为P,把△APB翻折,使点P落在线段AB上(不与A、B重合),记作P′,折痕为EF.分析 (1)设抛物线的解析式为y=a(x-2)(x-8)将C点坐标代入即可求得抛物线的解析式;
(2)根据抛物线的解析式y=$\frac{\sqrt{3}}{3}$x2-$\frac{10\sqrt{3}}{3}$x+$\frac{16\sqrt{3}}{3}$,求得顶点P(5,-3$\sqrt{3}$)得到AP=AB=BP=6,求得∠PAP′=60°,作P′G⊥AP于G,根据A(2,0),P′(4,0),得到AP′=2,求出AG=$\frac{1}{2}$AP′=1,P′G=$\sqrt{3}$,设P′E=PE=y,EG=6-1-y根据勾股定理列方程即可得到结论;
(3)先求出P点坐标,在Rt△P′EG中,根据勾股定理便可求出y关于x的函数关系式,分别令EP′⊥x轴、FP′⊥x轴、EF⊥x轴进行分类讨论,便可得出满足题意得P点坐标.
解答 解:(1)设抛物线的解析式为y=a(x-2)(x-8),
把C(0,$\frac{16\sqrt{3}}{3}$)代入得a=$\frac{\sqrt{3}}{3}$,
∴y=$\frac{\sqrt{3}}{3}$(x-2)(x-8)
即y=$\frac{\sqrt{3}}{3}$x2-$\frac{10\sqrt{3}}{3}$x+$\frac{16\sqrt{3}}{3}$;
(2)∵抛物线y=$\frac{\sqrt{3}}{3}$x2-$\frac{10\sqrt{3}}{3}$x+$\frac{16\sqrt{3}}{3}$顶点P(5,-3$\sqrt{3}$)
∴AP=AB=BP=6,
∴∠PAP′=60°,
作P′G⊥AP于G,
∵A(2,0),P′(4,0),
∴AP′=2,
∴AG=$\frac{1}{2}$AP′=1,P′G=$\sqrt{3}$,
设P′E=PE=y,EG=6-1-y
在Rt△P′EG中,($\sqrt{3}$)2+(6-1-y)2=y2
解得:y=2.8
∴P′E=PE=2.8;
(3)AP′=x,PE=y,∵顶点P(5,-3$\sqrt{3}$
AP=AB=BP=6,
∴∠PAP′=60°,
作P′G⊥AP于G,
则AG=$\frac{1}{2}$x,P′G=$\frac{\sqrt{3}}{2}$x
又P′E=PE=y,EG=6-$\frac{1}{2}$x-y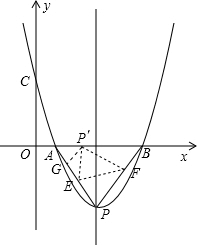
在Rt△P′EG中,($\frac{\sqrt{3}}{2}$x)2+(6-$\frac{1}{2}$x-y)2=y2,
∴y=$\frac{{x}^{2}-6x+36}{12-x}$(0<x<6)
①若EP′⊥x轴,则6-y=2x,6-$\frac{{x}^{2}-6x+36}{12-x}$=2x,
x1=12-6$\sqrt{3}$,x2=12+6$\sqrt{3}$(舍去),
∴P′(14-6$\sqrt{3}$,0)
②若FP′⊥x轴,则6-y=$\frac{1}{2}$x,6-$\frac{{x}^{2}-6x+36}{12-x}$=$\frac{1}{2}$x,
x3=6$\sqrt{3}$-6,x4=-6$\sqrt{3}$-6(舍去),
∴P′(6$\sqrt{3}$-4,0)
③若EF⊥x轴,显然不可能.
∴P′(14-6$\sqrt{3}$,0)或P′(6$\sqrt{3}$-4,0).
点评 本题是二次函数的综合题,其中涉及到的知识点有抛物线的公式的求法和勾股定理等知识点,是各地中考的热点和难点,解题时注意数形结合和分类讨论等数学思想的运用,同学们要加强训练,属于中档题.


 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案科目:初中数学 来源: 题型:解答题
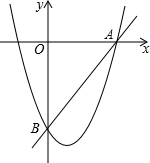 如图,抛物线y=x2+bx-4分别与x轴正半轴、y轴交于点A、B,且$tan∠OBA=\frac{3}{4}$.
如图,抛物线y=x2+bx-4分别与x轴正半轴、y轴交于点A、B,且$tan∠OBA=\frac{3}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com