
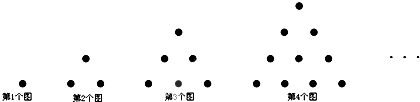
分析 由图形可知:摆第1个图形需1颗石子,摆第2个图形需1+2=3颗石子,摆第3个图形需1+2+3=6颗石子,摆第4个图形需1+2+3+4=10颗石子,…由此得出摆第n个图形需1+2+3+…+n=$\frac{1}{2}$n(n+1)颗石子,进一步代入求得答案即可.
解答 解:∵摆第1个图形需1颗石子,
摆第2个图形需1+2=3颗石子,
摆第3个图形需1+2+3=6颗石子,
摆第4个图形需1+2+3+4=10颗石子,
…
∴摆第n个图形需1+2+3+…+n=$\frac{1}{2}$n(n+1)颗石子,
∴摆第10个图形需$\frac{1}{2}$×10×(10+1)=55颗石子.
故答案为:55.
点评 此题考查图形的变化规律,找出图形之间的联系,得出数字的运算规律解决问题.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
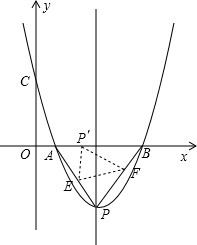 已知:抛物线经过A(2,0)、B(8,0)、C(0,$\frac{16\sqrt{3}}{3}$);设抛物线的顶点为P,把△APB翻折,使点P落在线段AB上(不与A、B重合),记作P′,折痕为EF.
已知:抛物线经过A(2,0)、B(8,0)、C(0,$\frac{16\sqrt{3}}{3}$);设抛物线的顶点为P,把△APB翻折,使点P落在线段AB上(不与A、B重合),记作P′,折痕为EF.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com