
����Ŀ����������һ����������һ�������ڶԱ��ཻ�������뽻��֮����߶ΰ���������ηָ������С�����Σ�����ֵõ�����С��������һ��Ϊ���������Σ���һ����ԭ���������ƣ����ǰ������߶ν�����������ε������ߣ�
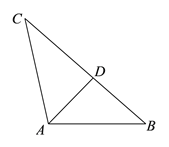
��1����ͼ���ڡ�ABC�У�ADΪ��ƽ���ߣ���B=50������C=30������֤��ADΪ��ABC����������
��2���ڡ�ABC�У���B=46����AD�ǡ�ABC�������ߣ��ҡ�ABD����ABΪ���ĵ��������Σ����BAC�Ķ�����
��3���ڡ�ABC�У�AB=4��AC=2��AD�ǡ�ABC�������ߣ��ҡ�ABD�ǵ��������Σ�ֱ��д��������AD�ij���
���𰸡�(1)��������(2) 113����(3) ![]() ��
��![]()
���������������:(1)���������ε������ߵĶ���,ֻҪ֤����ABD�ǵ���������,
��CAD����CBA���ɽ������,(2)��ͼ2��,���������������������AB=AD,
��CAD�ס�CBA,����B=��ADB=��CAD,��AC��BC,������ABC�������ì��, ����AB=BD, ��CAD�ס�CBA, (3)��ͼ3��,������������������AD=BD, ��CAD�ס�CBA,��![]() ��BD=AD=x,CD=y,�ɵ�
��BD=AD=x,CD=y,�ɵ�![]() ,�ⷽ�̼���, ����AB=AD=4,��
,�ⷽ�̼���, ����AB=AD=4,��![]() ,��BD=AD=x,CD=y,�ɵ�
,��BD=AD=x,CD=y,�ɵ�![]() ,�ⷽ�̼���, ����AB=AD,��Ȼ������.
,�ⷽ�̼���, ����AB=AD,��Ȼ������.
(1)֤����
�ߡ�B=50������C=30�������BAC=100����
��ADƽ�֡�BAC��
���BAD=��DAC=50����
���B=��BAD=50������DB=DA��
���ABD�ǵ��������Σ�
�ߡ�C=��C����DAC=��B=50����
���CAD�ס�CBA��
���߶�AD�ǡ�ABC�������ߣ�
��2����AB=AD����ȥ��
����������CAD�ס�CBA�����B=��ADB=��CAD����AC��BC����
��AB=BD����B=46����
���BAD=��BDA=67����
�ߡ�CAD�ס�CBA��
���CAD=��B=46����
���BAC=67��+46��=113����
��3��![]() ��
��![]() .
.


 ���ٴ�����ɽ����ϵ�д�
���ٴ�����ɽ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() ��ƽ���ߣ�
��ƽ���ߣ�![]() ��
��![]() ����
����![]() ��
��![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �����ۢ�
�����ۢ�![]() ����
����![]() ����
����![]() ����
����![]() .������ȷ���У� ��
.������ȷ���У� ��
A.4��B.3��C.2��D.1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
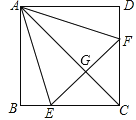
����Ŀ����ͼ,������ABCD�У���E��F�ֱ���BC��CD�ϣ� ��AEF�ǵȱ������Σ�����AC��EF�ڵ�G�����н���:��CE��CF���ڡ�AEB��75�㣬��AG��2GC����BE��DF��EF,��S��CEF��2S��ABE�����н�����ȷ�ĸ���Ϊ( )
A. 2�� B. 3�� C. 4�� D. 5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
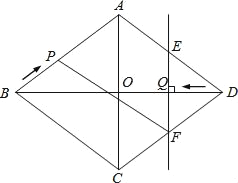
����Ŀ����ͼ��������ABCD�У�AC��BD���ڵ�O����AC=12cm��BD=16cm����P�ӵ�B��������BA���������˶����ٶ�Ϊlcm/s��ͬʱ��ֱ��EF�ӵ�D��������DB���������˶����ٶ�Ϊlcm/s��EF��BD������AD��BD��CD�ֱ��ڵ�E��Q��F����ֱ��EFֹͣ�˶�ʱ����PҲֹͣ�˶�������PF�����˶�ʱ��Ϊt��s����0��t��8��������������⣺
��1��������ABCD�������
��2����t=1ʱ����QF����
��3���Ƿ����ijһʱ��t��ʹ�ı���APFD��ƽ���ı��Σ������ڣ����tֵ���������ڣ���˵�����ɣ�
��4������DEF�����Ϊs��cm2�������ú�t�Ĵ���ʽ��ʾS������tΪ��ֵʱ����DEF���������BPC�������ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
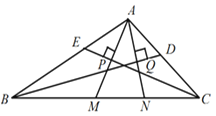
����Ŀ����1����ͼ����ʾ����ACB=��POQ=��XOB=90�㣮
����֤����POA=��XOQ��
���жϡ�PAO�͡�QXO�Ƿ����ƣ����������������������֤�����粻���ƣ�˵�����ɣ�
��2����ͼ�ڣ��ڡ�ABC�У���ACB=90�㣬��CBA=30�㣬AO=BO����P��AC�ϣ���Q��BC�ϣ��ҡ�POQ=90�㣬XO��AB��BC��X��AC=4cm��AP=x��0��x��4�������PCQ�����Ϊy����y��x�ĺ�����ϵʽ��
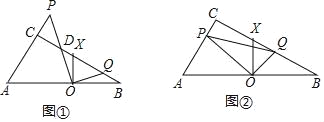
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У�EΪCD���е㣬AE�Ĵ�ֱƽ���߷ֱ�AD��BC��AB���ӳ����ڵ�F��G��H������HE��HC��OD������CO���ӳ���AD�ڵ�M�������н����У�
��FG=2AO����OD��HE����![]() ����2OE2=AHDE����GO+BH=HC
����2OE2=AHDE����GO+BH=HC
��ȷ���۵ĸ����У�������
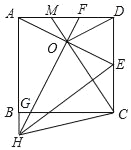
A. 2 B. 3 C. 4 D. 5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㶼�ڸ���ϵĵ������ν�����������Σ���ͼ����![]() �ķ���ֽ�У�
�ķ���ֽ�У�![]() �Ǹ�������Σ�
�Ǹ�������Σ�
��1����ͼ![]() �У��Ե�
�У��Ե�![]() Ϊ�Գ����ģ�����һ����
Ϊ�Գ����ģ�����һ����![]() �����ĶԳƵĸ��������
�����ĶԳƵĸ��������![]() ��������������ֱ��д��
��������������ֱ��д��![]() ��
��![]() ��λ�ù�ϵ�� ��
��λ�ù�ϵ�� ��
��2����ͼ![]() �У���
�У���![]() ���ڵ�ֱ��Ϊ�Գ��ᣬ����һ����
���ڵ�ֱ��Ϊ�Գ��ᣬ����һ����![]() ����ԳƵĸ��������
����ԳƵĸ��������![]() ��������������ֱ��д��
��������������ֱ��д��![]() ��ʲô��״�����������Σ� ��
��ʲô��״�����������Σ� ��
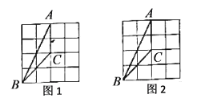
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ķ�˼�����Ķ����в��ϣ�
��֪��x��y��2����x��1��y��0����ȷ��x+y��ȡֵ��Χ�������½ⷨ��
�⣺��x��y��2��
��x��y+2
�֡�x��1
��y+2��1
��y����1
�֡�y��0
�ੁ1��y��0 ��
ͬ��1��x ��2 ��
�ɢ�+�ڵé�1+1��x+y��0+2
��x+y ��ȡֵ��Χ��0��x+y ��2
������Ӧ�ã��밴����������������������⣺
��֪x ��y ��3����x �� 2��y ��1����x+y��ȡֵ��Χ�� ��
����չ�ƹ㣩�밴����������������������⣺
��֪x+y��2����x��1��y����4����ȷ��x��y��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com