
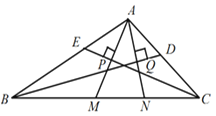
【题目】如图,在![]() 中,
中,![]() 、
、![]() 分别是
分别是![]() 和
和![]() 的平分线,
的平分线,![]() 于
于![]() ,交
,交![]() 于
于![]() ,
,![]() 于
于![]() ,交
,交![]() 于
于![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,结论①
,结论①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确的有( )
.其中正确的有( )
A.4个B.3个C.2个D.1个
【答案】B
【解析】
①根据三角形的内角和定理判定∠CAM=∠CMA,由等腰三角形的判定和三线合一的性质可得结论正确;
②根据BN=AB=6,CM=AC=5,及线段的和与差可得BC的长;
③根据三角形的内角和定理及角的和与差可得结论;
④要想得到AM=AN,必有∠AMN=∠ANM,而AB≠AC,可知∠ABC≠∠ACB,从而得AM≠AN.
解:①∵CE平分∠ACE,
∴∠ACP=∠MCP,
∵AM⊥CE,
∴∠APC=∠MPC=90°,
∴∠CAM=∠CMA,
∴AC=CM,
∴AP=PM,
①正确;
②同理得:BN=AB=6,
∵CM=AC=5,
∴BC=BN+CM-MN=6+5-2=9,
②正确;
③∵∠BAC=∠MAC+∠BAN-∠MAN=110°,
由①知:∠CMA=∠CAM,∠BNA=∠BAN,
△AMN中,∠CMA+∠BNA=180°-∠MAN=∠BAN+∠MAC,
∴180°-∠MAN-∠MAN=110°,
∴∠MAN=35°,
③正确;
④当∠AMN=∠ANM时,AM=AN,
∵AB=6≠AC=5
∴∠ABC≠∠ACB,
∴∠AMN≠∠ANM,则AM与AN不相等,
④不正确;
所以本题不正确的有④,
故选:B.


科目:初中数学 来源: 题型:
【题目】如图1,将等腰△ABC沿对称轴折叠后,得到△ADC(△ADB),若![]() ,则称等腰△ABC为“长月三角形”ABC.
,则称等腰△ABC为“长月三角形”ABC.

(1)结合题目情境,请你判断“长月三角形”一定会是______三角形.
(2)如图2,C为线段AB上一点,分别以AC和BC为边作“长月三角形”ACD和“长月三角形”BCE,连接AE、BD交于点O,AE与CD交于点P,CE与BD交于点M.
①求证:![]() ;
;
②求![]() 的度数.
的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边![]() 中,边长为
中,边长为![]() .点
.点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向运动,速度为
方向运动,速度为![]() ;同时点
;同时点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向运动,速度为
方向运动,速度为![]() ,当两个点有一个点到达终点时,另一个点随之停止运动.设运动时间为
,当两个点有一个点到达终点时,另一个点随之停止运动.设运动时间为![]() ,解答下列问题:
,解答下列问题:
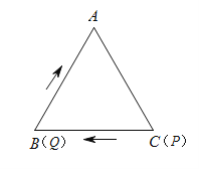
(1)当![]() 时,
时,![]() _______(用含
_______(用含![]() 的代数式表示);
的代数式表示);
(2)当![]() 时,求
时,求![]() 的值,并直接写出此时
的值,并直接写出此时![]() 为什么特殊的三角形?
为什么特殊的三角形?
(3)当![]() ,且
,且![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=﹣x2+bx+c的图象经过坐标原点,且与x轴交于A(﹣2,0).
(1)求此二次函数解析式及顶点B的坐标;
(2)在抛物线上有一点P,满足S△AOP=3,直接写出点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 为等边三角形,
为等边三角形,![]() 为
为![]() 上的一个动点,
上的一个动点,![]() 为
为![]() 延长线上一点,且
延长线上一点,且![]() .
.
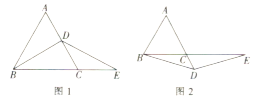
(1)当![]() 是
是![]() 的中点时,求证:
的中点时,求证:![]() .
.
(2)如图1,若点![]() 在边
在边![]() 上,猜想线段
上,猜想线段![]() 与
与![]() 之间的关系,并说明理由.
之间的关系,并说明理由.
(3)如图2,若点![]() 在
在![]() 的延长线上,(1)中的结论是否仍然成立,请说明理由.
的延长线上,(1)中的结论是否仍然成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,如果BD,CE分别是∠ABC,∠ACB的平分线且他们相交于点P,设∠A=n°.
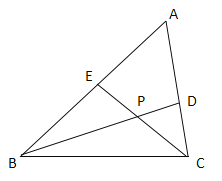
(1)求∠BPC的度数(用含n的代数式表示),写出推理过程.
(2)当∠BPC=125°时,∠A= .
(3)当n=60°时,EB=7,BC=12,DC的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个二次函数的图象经过(﹣1,﹣1),(0,0),(1,9)三点
(1)求这个二次函数的解析式.
(2)若另外三点(x1,21),(x2,21),(x1+x2,n)也在该二次函数图象上,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰直角三角形![]() 中,
中,![]() ,
,![]() ,
,![]() .将等腰直角形
.将等腰直角形![]() 沿高
沿高![]() 剪开后,拼成图2所示的正方形
剪开后,拼成图2所示的正方形![]() .
.
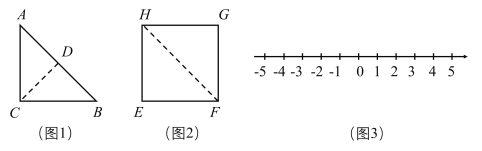
(1)如图1,等腰直角三角形![]() 的面积是______________.
的面积是______________.
(2)如图2,求正方形![]() 的边长是多少?
的边长是多少?
(3)把正方形![]() 放到数轴上(如图3),使得边
放到数轴上(如图3),使得边![]() 落到数轴上,其中一个端点所对应的数为-1,直接写出另一个端点所对应的数.
落到数轴上,其中一个端点所对应的数为-1,直接写出另一个端点所对应的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 的对称轴为
的对称轴为![]() 轴,且经过(0,0),(
轴,且经过(0,0),(![]() )两点,点P在抛物线上运动,以P为圆心的⊙P经过定点A(0,2),
)两点,点P在抛物线上运动,以P为圆心的⊙P经过定点A(0,2),
(1)求![]() 的值;
的值;
(2)求证:点P在运动过程中,⊙P始终与![]() 轴相交;
轴相交;
(3)设⊙P与![]() 轴相交于M
轴相交于M![]() ,N
,N ![]() (
(![]() <
<![]() )两点,当△AMN为等腰三角形时,求圆心P的纵坐标.
)两点,当△AMN为等腰三角形时,求圆心P的纵坐标.
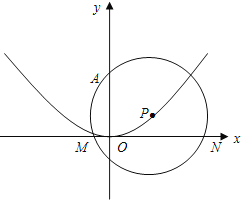
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com