
【题目】如图,在△ABC中,如果BD,CE分别是∠ABC,∠ACB的平分线且他们相交于点P,设∠A=n°.
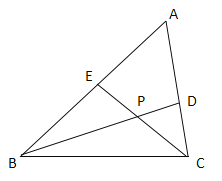
(1)求∠BPC的度数(用含n的代数式表示),写出推理过程.
(2)当∠BPC=125°时,∠A= .
(3)当n=60°时,EB=7,BC=12,DC的长为 .
【答案】(1)∠BPC=90°+![]() n,推理过程见解析;(2)70°;(3)5.
n,推理过程见解析;(2)70°;(3)5.
【解析】
(1)根据角平分线的性质得∠ABC=2∠PBC,∠ACB=2∠PCB,再根据三角形内角和定理求得∠A=-180°+2∠BPC,即可求证∠BPC=90°+![]() n;
n;
(2)根据(1)可知∠BPC=90°+![]() n,把∠BPC=125°代入原式求出n即为∠A的度数;
n,把∠BPC=125°代入原式求出n即为∠A的度数;
(3)当n=60°时,即可求出∠BPC=120°,作辅助线在CB上截取CG=CD,可证出△CPG≌△PCD(SAS),即可得出∠DPO=∠GPC,PD=PG,再可证出△BEP≌△BGP,即可得出BE=BG,即可求出DC.
解:(1)∵DB、CE分别为∠ABC,∠ACB的平分线,
∴∠ABC=2∠PBC,∠ACB=2∠PCB.
∵∠A=180°-(∠ABC+∠ACB),
∴∠A=180°-2(∠PBC+∠PCB),
∴∠A=180°-2(180°-∠BPC),
∴∠A=-180°+2∠BPC,
∴2∠BPC=180°+∠A,
∴∠BPC=90°+![]() ∠A,
∠A,
∴∠BPC=90°+![]() n
n
(2)由(1)知∠BPC=90°+![]() ∠A
∠A
∴当∠BPC=125°时,∠A =2×(125°-90°)= 70°;
(3)在CB上截取CG=CD,连接GP,
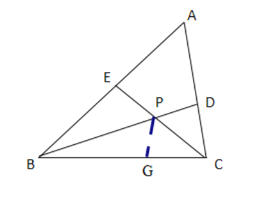
![]() CE平分
CE平分![]()
∴∠GCP=∠PCD,
在△PCD和△PCG中,
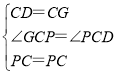
∴△PCD≌△CGP(SAS),
∴∠GPC=∠CPD,PG=PD,
由∠BPG+∠GPC=120°,
又∵∠BPG+2∠GPC=180°,
解得:∠BPG=∠GPC=∠FPC=60°
在△BEP和△BGP中,
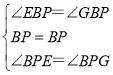
∴△BEP≌△BGP(ASA),
∴BE=BG,
∴CG=BC-BG=BC-BE=12-7=5
∴CD=CG=5.


科目:初中数学 来源: 题型:
【题目】下列说法中正确的有( )个
①对角线互相平分的四边形是平行四边形;②等腰梯形在同一底上的两个内角相等;
③对角线互相垂直的四边形是菱形;④一组邻边相等的矩形是正方形.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
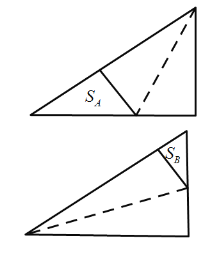
【题目】如图是两个全等的三角形纸片,其三边长之比为![]() ,按图中方法分别将其对折,使折痕(图中虚线)过其中的一个顶点,且使该项点所在两边重合,记折叠后不重叠部分面积分别为
,按图中方法分别将其对折,使折痕(图中虚线)过其中的一个顶点,且使该项点所在两边重合,记折叠后不重叠部分面积分别为![]() ,已知
,已知![]() ,则纸片的面积是( )
,则纸片的面积是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应国家的号召,减少污染,某厂家生产出一种节能又环保的油电混合动力汽车,既可以用油做动力行驶,也可以用电做动力行驶.这种油电混合动力汽车从甲地行驶到乙地,若完全用油做动力行驶,费用为108元;若完全用电做动力行驶,费用为36元,已知汽车行驶中每千米用油的费用比用电的费用多0.6元.
(1)求汽车行驶中每千米用电的费用和甲、乙两地之间的距离.
(2)若汽车从甲地到乙地采用油电混合动力行驶,且所需费用不超过60元,则至少需要用电行驶多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场服装部为了调动营业员的积极性,决定实行目标管理,根据目标完成的情况对营业员进行适当的奖励.为了确定一个适当的月销售目标,商场服装部统计了每位营业员在某月的销售额(单位:万元),数据如下:
17 | 18 | 16 | 13 | 24 | 15 | 28 | 26 | 18 | 19 |
22 | 17 | 16 | 19 | 32 | 30 | 16 | 14 | 15 | 26 |
15 | 32 | 23 | 17 | 15 | 15 | 28 | 28 | 16 | 19 |
对这30个数据按组距3进行分组,并整理、描述和分析如下.
频数分布表
组别 | 一 | 二 | 三 | 四 | 五 | 六 | 七 |
销售额 |
|
|
|
|
|
|
|
频数 | 7 | 9 | 3 |
| 2 |
| 2 |
数据分析表
平均数 | 众数 | 中位数 |
20.3 |
| 18 |
请根据以上信息解答下列问题:
(1)填空:a= ,b= ,c= ;
(2)若将月销售额不低于25万元确定为销售目标,则有 位营业员获得奖励;
(3)若想让一半左右的营业员都能达到销售目标,你认为月销售额定为多少合适?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第一袋里有红球和白球共![]() 个,第二袋里的红球比白球多
个,第二袋里的红球比白球多![]() 个,每个球除颜色外都相同.把其中一个袋子里的球倒入另一个袋里混合后.任意摸出一个球是白球的可能性和任意摸出一个红球的可能性一样大,问第一个袋子里的红球和白球各几个?
个,每个球除颜色外都相同.把其中一个袋子里的球倒入另一个袋里混合后.任意摸出一个球是白球的可能性和任意摸出一个红球的可能性一样大,问第一个袋子里的红球和白球各几个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标中,边长为2的正方形![]() 的两顶点
的两顶点![]() 、
、![]() 分别在
分别在![]() 轴、
轴、![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在原点.现将正方形
在原点.现将正方形![]() 绕
绕![]() 点顺时针旋转,当
点顺时针旋转,当![]() 点第一次落在直线
点第一次落在直线![]() 上时停止旋转,旋转过程中,
上时停止旋转,旋转过程中,![]() 边交直线
边交直线![]() 于点
于点![]() ,
,![]() 边交
边交![]() 轴于点
轴于点![]()

(1)求边![]() 在旋转过程中所扫过的面积;
在旋转过程中所扫过的面积;
(2)旋转过程中,当![]() 和
和![]() 平行时,求正方形
平行时,求正方形![]() 旋转的度数;
旋转的度数;
(3)设![]() 的周长为
的周长为![]() ,在旋转正方形
,在旋转正方形![]() 的过程中,
的过程中,![]() 值是否有变化?请证明你的结论.
值是否有变化?请证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1)所示,在Rt△ABC中,∠B=90°,AB=4,BC=3,将△ABC沿着AC翻折得到△ADC,如图(2),将△ADC绕着点A旋转到△AD′C′,连接CD′,当CD′∥AB时,四边形ABCD的面积为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com