
【题目】如图1,将等腰△ABC沿对称轴折叠后,得到△ADC(△ADB),若![]() ,则称等腰△ABC为“长月三角形”ABC.
,则称等腰△ABC为“长月三角形”ABC.

(1)结合题目情境,请你判断“长月三角形”一定会是______三角形.
(2)如图2,C为线段AB上一点,分别以AC和BC为边作“长月三角形”ACD和“长月三角形”BCE,连接AE、BD交于点O,AE与CD交于点P,CE与BD交于点M.
①求证:![]() ;
;
②求![]() 的度数.
的度数.

【答案】(1)等边;(2)①见解析;②120°
【解析】
(1)利用等腰三角形性质以及含30°的直角三角形进行判断即可.
(2)①利用(1)中结论,易证![]() ,即可解答;
,即可解答;
②利用全等三角形对应角相等的性质,即可解答.
(1)等边;
证明:∵将等腰△ABC沿对称轴折叠
∴AD⊥CD ∴△ADC为直角三角形
∵![]()
∴∠A=30°,∠C=60°
∴等腰△ABC为等边三角形.
∴“长月三角形”一定会是等边三角形.
(2)①由(1)可知,△ACD和△BCE是等边三角形
∴AC=CD,CE=CB,∠ACD=∠BCE=60°
∴∠ACD+∠DCE=∠BCE+∠DCE 即∠ACE=∠BCD
在![]() 和
和![]() 中,
中,
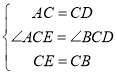
∴![]()
∴AE=BD
②∵![]()
∴∠CAE=∠CDB
∵∠DCA=∠CDB+∠DBC=60°
∴∠DOA=∠CAE+∠DBC=60°
∵∠DOA+∠AOB=180°
∴∠AOB=120°


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,Rt△BAP中,∠BAP=90°,已知∠CBO=∠ABP,BP交AC于点O,E为AC上一点,且AE=OC.
(1)求证:AP=AO;
(2)求证:PE⊥AO;
(3)当AE=![]() AC,AB=10时,求线段BO的长度.
AC,AB=10时,求线段BO的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
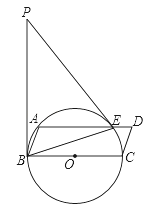
【题目】如图,BC为⊙O的直径,A为⊙O上的点,以BC、AB为边作ABCD,⊙O交AD于点E,连结BE,点P为过点B的⊙O的切线上一点,连结PE,且满足∠PEA=∠ABE.
(1)求证:PB=PE;
(2)若sin∠P=![]() , 求
, 求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
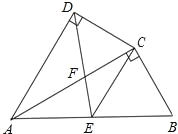
【题目】如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,
(1)求证:AC2=ABAD;
(2)求证:△AFD∽△CFE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的有( )个
①对角线互相平分的四边形是平行四边形;②等腰梯形在同一底上的两个内角相等;
③对角线互相垂直的四边形是菱形;④一组邻边相等的矩形是正方形.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
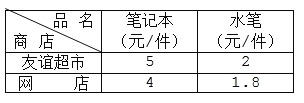
【题目】某班为准备半期考表彰的奖品,计划从友谊超市购买笔记本和水笔共40件.在获知某网店有“双十一”促销活动后,决定从该网店购买这些奖品.已知笔记本和水笔在这两家商店的零售价分别如下表,且在友谊超市购买这些奖品需花费125元.
(1)班级购买的笔记本和水笔各多少件?
(2)求从网店购买这些奖品可节省多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,函数![]() 的图像与
的图像与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,与函数
,与函数![]() 的图像交于点
的图像交于点![]() ,点
,点![]() 的横坐标为
的横坐标为![]() .
.
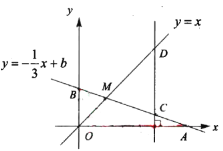
(1)求点![]() 的坐标;
的坐标;
(2)在![]() 轴上有一动点
轴上有一动点![]() .
.
①若三角形![]() 是以
是以![]() 为底边的等腰三角形,求
为底边的等腰三角形,求![]() 的值;
的值;
②过点![]() 作
作![]() 轴的垂线,分别交函数
轴的垂线,分别交函数![]() 和
和![]() 的图像于点
的图像于点![]() 、
、![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com