
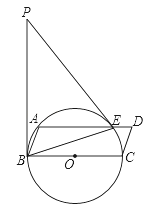
【题目】如图,BC为⊙O的直径,A为⊙O上的点,以BC、AB为边作ABCD,⊙O交AD于点E,连结BE,点P为过点B的⊙O的切线上一点,连结PE,且满足∠PEA=∠ABE.
(1)求证:PB=PE;
(2)若sin∠P=![]() , 求
, 求![]() 的值.
的值.
【答案】(1)证明见解析;(2)![]() ;
;
【解析】
(1)根据切线的性质求得∠ABP=∠AEB,根据已知条件即可求得∠PBE=∠PEB,根据等角对等边即可证明结论;
(2)连接EC,延长DA交PB于F,根据平行弦的性质得出![]() ,进而求得AB=CE=CD,得出三角形CED是等腰三角形,在等腰三角形PBE中根据勾股定理求得BE的长,进而求得
,进而求得AB=CE=CD,得出三角形CED是等腰三角形,在等腰三角形PBE中根据勾股定理求得BE的长,进而求得![]() ,由于∠AEB=∠EBC,∠ABP=∠AEB,得出∠ABP=∠EBC,从而得出∠PBE=∠ABC=∠D,求得△CDE∽△PBE,得出
,由于∠AEB=∠EBC,∠ABP=∠AEB,得出∠ABP=∠EBC,从而得出∠PBE=∠ABC=∠D,求得△CDE∽△PBE,得出![]() .
.
(1)证明:∵PB是⊙O的切线,
∴∠ABP=∠AEB,
∵∠PEA=∠ABE.
∴∠PBE=∠PEB,
∴PB=PE;
(2)连接EC,延长DA交PB于F,
∵PB是⊙O的切线,
∴BC⊥PB,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴EF⊥PB,
∵sin∠P=![]() ,
,
设PE=5a,EF=3a,则PF=4a,
∵PB=PE=5a,
∴BF=a,
∴BE=![]() ,
,
∴![]() ,
,
∵AD∥BC,
∴![]() ,
,
∴AB=CE,
∵AB=CD,
∴CE=CD,
∴∠D=∠CED,
∵AD∥BC,
∴∠AEB=∠EBC,
∵∠ABP=∠AEB,
∴∠ABP=∠EBC,
∴∠PBE=∠ABC,
∴∠PBE=∠D,
∵∠PBE=∠PEB,
∴△CDE∽△PBE,
∴![]() .
.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,![]() ,
,![]() ,
,![]() .
.
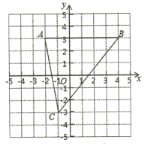
(1)点![]() 到
到![]() 轴的距离为:______;
轴的距离为:______;
(2)![]() 的三边长为:
的三边长为:![]() ______,
______,![]() ______,
______,![]() ______;
______;
(3)当点![]() 在
在![]() 轴上,且
轴上,且![]() 的面积为6时,点
的面积为6时,点![]() 的坐标为:______.
的坐标为:______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数![]() 的图像为直线
的图像为直线![]() .
.
(1)若直线![]() 与正比例函数
与正比例函数![]() 的图像平行,且过点(0,2),求直线
的图像平行,且过点(0,2),求直线![]() 的函数表达式;
的函数表达式;
(2)若直线![]() 过点(3,0),且与两坐标轴围成的三角形面积等于3,求
过点(3,0),且与两坐标轴围成的三角形面积等于3,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】位于南岸区黄桷垭的文峰塔,有着“平安宝塔”之称.某校数学社团对其高度 AB进行了测量.如图,他们从塔底A的点B出发,沿水平方向行走了13米,到达点C,然后沿斜坡CD继续前进到达点D处,已知DC=BC.在点D处用测角仪测得塔顶A的仰角为42°(点A,B,C,D,E在同一平面内).其中测角仪及其支架DE高度约为0.5米,斜坡CD的坡度(或坡比)i=1:2.4,那么文峰塔的高度AB约为( )(sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)

A. 22.5 米 B. 24.0 米 C. 28.0 米 D. 33.3 米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),一架云梯AB斜靠在一竖直的墙上,云梯的顶端A距地面15米,梯子的长度比梯子底端B离墙的距离大5米.
(1)这个云梯的底端B离墙多远?
(2)如图(2),如果梯子的顶端下滑了8m(AC的长),那么梯子的底部在水平方向右滑动了多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了树立文明乡风,推进社会主义新农村建设,某村决定组建村民文体团队,现围绕“你最喜欢的文体活动项目(每人仅限一项)”,在全村范围内随机抽取部分村民进行问卷调查,并将调查结果绘制成如下两幅不完整的统计图.请你根据统计图解答下列问题:

(1)这次参与调查的村民人数为 人;
(2)请将条形统计图补充完整;
(3)求扇形统计图中“划龙舟”所在扇形的圆心角的度数;
(4)若在“广场舞、腰鼓、花鼓戏、划龙舟”这四个项目中任选两项组队参加端午节庆典活动,请用列表或画树状图的方法,求恰好选中“花鼓戏、划龙舟”这两个项目的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线F:y=x2+bx+c的图象经过坐标原点O,且与x轴另一交点为(﹣![]() ,0).
,0).

(1)求抛物线F的解析式;
(2)如图1,直线l:y=![]() x+m(m>0)与抛物线F相交于点A(x1,y1)和点B(x2,y2)(点A在第二象限),求y2﹣y1的值(用含m的式子表示);
x+m(m>0)与抛物线F相交于点A(x1,y1)和点B(x2,y2)(点A在第二象限),求y2﹣y1的值(用含m的式子表示);
(3)在(2)中,若m=![]() ,设点A′是点A关于原点O的对称点,如图2.
,设点A′是点A关于原点O的对称点,如图2.
①判断△AA′B的形状,并说明理由;
②平面内是否存在点P,使得以点A、B、A′、P为顶点的四边形是菱形?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将等腰△ABC沿对称轴折叠后,得到△ADC(△ADB),若![]() ,则称等腰△ABC为“长月三角形”ABC.
,则称等腰△ABC为“长月三角形”ABC.

(1)结合题目情境,请你判断“长月三角形”一定会是______三角形.
(2)如图2,C为线段AB上一点,分别以AC和BC为边作“长月三角形”ACD和“长月三角形”BCE,连接AE、BD交于点O,AE与CD交于点P,CE与BD交于点M.
①求证:![]() ;
;
②求![]() 的度数.
的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边![]() 中,边长为
中,边长为![]() .点
.点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向运动,速度为
方向运动,速度为![]() ;同时点
;同时点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向运动,速度为
方向运动,速度为![]() ,当两个点有一个点到达终点时,另一个点随之停止运动.设运动时间为
,当两个点有一个点到达终点时,另一个点随之停止运动.设运动时间为![]() ,解答下列问题:
,解答下列问题:
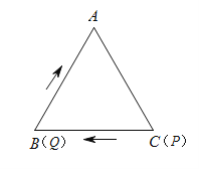
(1)当![]() 时,
时,![]() _______(用含
_______(用含![]() 的代数式表示);
的代数式表示);
(2)当![]() 时,求
时,求![]() 的值,并直接写出此时
的值,并直接写出此时![]() 为什么特殊的三角形?
为什么特殊的三角形?
(3)当![]() ,且
,且![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com