
【题目】已知抛物线F:y=x2+bx+c的图象经过坐标原点O,且与x轴另一交点为(﹣![]() ,0).
,0).

(1)求抛物线F的解析式;
(2)如图1,直线l:y=![]() x+m(m>0)与抛物线F相交于点A(x1,y1)和点B(x2,y2)(点A在第二象限),求y2﹣y1的值(用含m的式子表示);
x+m(m>0)与抛物线F相交于点A(x1,y1)和点B(x2,y2)(点A在第二象限),求y2﹣y1的值(用含m的式子表示);
(3)在(2)中,若m=![]() ,设点A′是点A关于原点O的对称点,如图2.
,设点A′是点A关于原点O的对称点,如图2.
①判断△AA′B的形状,并说明理由;
②平面内是否存在点P,使得以点A、B、A′、P为顶点的四边形是菱形?若存在,求出点P的坐标;若不存在,请说明理由.
【答案】(1)y=x2+![]() x;(2)y2﹣y1=
x;(2)y2﹣y1=![]() ;(3)①△AA′B为等边三角形,理由见解析;②平面内存在点P,使得以点A、B、A′、P为顶点的四边形是菱形,点P的坐标为(2
;(3)①△AA′B为等边三角形,理由见解析;②平面内存在点P,使得以点A、B、A′、P为顶点的四边形是菱形,点P的坐标为(2![]() ,
,![]() )、(﹣
)、(﹣![]() )和(﹣
)和(﹣![]() ,﹣2)
,﹣2)
【解析】
(1)根据点的坐标,利用待定系数法即可求出抛物线F的解析式;
(2)将直线l的解析式代入抛物线F的解析式中,可求出x1、x2的值,利用一次函数图象上点的坐标特征可求出y1、y2的值,做差后即可得出y2-y1的值;
(3)根据m的值可得出点A、B的坐标,利用对称性求出点A′的坐标.
①利用两点间的距离公式(勾股定理)可求出AB、AA′、A′B的值,由三者相等即可得出△AA′B为等边三角形;
②根据等边三角形的性质结合菱形的性质,可得出存在符合题意得点P,设点P的坐标为(x,y),分三种情况考虑:(i)当A′B为对角线时,根据菱形的性质(对角线互相平分)可求出点P的坐标;(ii)当AB为对角线时,根据菱形的性质(对角线互相平分)可求出点P的坐标;(iii)当AA′为对角线时,根据菱形的性质(对角线互相平分)可求出点P的坐标.综上即可得出结论.
(1)∵抛物线y=x2+bx+c的图象经过点(0,0)和(﹣![]() ,0),
,0),
∴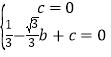 ,解得:
,解得: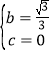 ,
,
∴抛物线F的解析式为y=x2+![]() x.
x.
(2)将y=![]() x+m代入y=x2+
x+m代入y=x2+![]() x,得:x2=m,
x,得:x2=m,
解得:x1=﹣![]() ,x2=
,x2=![]() ,
,
∴y1=﹣![]() +m,y2=
+m,y2=![]() +m,
+m,
∴y2﹣y1=(![]() +m)﹣(﹣
+m)﹣(﹣![]() +m)=
+m)=![]() (m>0).
(m>0).
(3)∵m=![]() ,
,
∴点A的坐标为(﹣![]() ,
,![]() ),点B的坐标为(
),点B的坐标为(![]() ,2).
,2).
∵点A′是点A关于原点O的对称点,
∴点A′的坐标为(![]() ,﹣
,﹣![]() ).
).
①△AA′B为等边三角形,理由如下:
∵A(﹣![]() ,
,![]() ),B(
),B(![]() ,2),A′(
,2),A′(![]() ,﹣
,﹣![]() ),
),
∴AA′=![]() ,AB=
,AB=![]() ,A′B=
,A′B=![]() ,
,
∴AA′=AB=A′B,
∴△AA′B为等边三角形.
②∵△AA′B为等边三角形,
∴存在符合题意的点P,且以点A、B、A′、P为顶点的菱形分三种情况,设点P的坐标为(x,y).
(i)当A′B为对角线时,有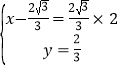 ,
,
解得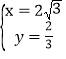 ,
,
∴点P的坐标为(2![]() ,
,![]() );
);
(ii)当AB为对角线时,有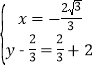 ,
,
解得: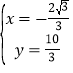 ,
,
∴点P的坐标为(﹣![]() ,
,![]() );
);
(iii)当AA′为对角线时,有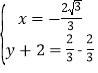 ,
,
解得: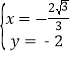 ,
,
∴点P的坐标为(﹣![]() ,﹣2).
,﹣2).
综上所述:平面内存在点P,使得以点A、B、A′、P为顶点的四边形是菱形,点P的坐标为(2![]() ,
,![]() )、(﹣
)、(﹣![]() )和(﹣
)和(﹣![]() ,﹣2).
,﹣2).


科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的边长为20cm,∠ABC=120°.动点P、Q同时从点A出发,其中P以4cm/s的速度,沿A→B→C的路线向点C运动;Q以2![]() cm/s的速度,沿A→C的路线向点C运动.当P、Q到达终点C时,整个运动随之结束,设运动时间为t秒.
cm/s的速度,沿A→C的路线向点C运动.当P、Q到达终点C时,整个运动随之结束,设运动时间为t秒.
(1)在点P、Q运动过程中,请判断PQ与对角线AC的位置关系,并说明理由;
(2)若点Q关于菱形ABCD的对角线交点O的对称点为M,过点P且垂直于AB的直线l交菱形ABCD的边AD(或CD)于点N.
①当t为何值时,点P、M、N在一直线上?
②当点P、M、N不在一直线上时,是否存在这样的t,使得△PMN是以PN为一直角边的直角三角形?若存在,请求出所有符合条件的t的值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
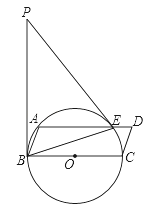
【题目】如图,BC为⊙O的直径,A为⊙O上的点,以BC、AB为边作ABCD,⊙O交AD于点E,连结BE,点P为过点B的⊙O的切线上一点,连结PE,且满足∠PEA=∠ABE.
(1)求证:PB=PE;
(2)若sin∠P=![]() , 求
, 求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
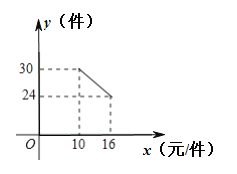
【题目】一名在校大学生利用“互联网+”自主创业,销售一种产品,这种产品成本价10元/件,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于16元/件,市场调查发现,该产品每天的销售量y(件)与销售价x(元/件)之间的函数关系如图所示.
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)求每天的销售利润W(元)与销售价x(元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
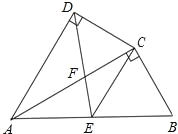
【题目】如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,
(1)求证:AC2=ABAD;
(2)求证:△AFD∽△CFE.
查看答案和解析>>
科目:初中数学 来源: 题型:
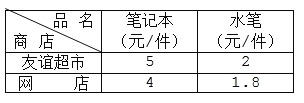
【题目】某班为准备半期考表彰的奖品,计划从友谊超市购买笔记本和水笔共40件.在获知某网店有“双十一”促销活动后,决定从该网店购买这些奖品.已知笔记本和水笔在这两家商店的零售价分别如下表,且在友谊超市购买这些奖品需花费125元.
(1)班级购买的笔记本和水笔各多少件?
(2)求从网店购买这些奖品可节省多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC 中,∠ABC和∠ACB的平分线交于点O,过点O作EF∥BC,交AB于点E,交AC于点F.
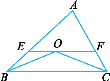
(1)若∠ABC=40°,∠ACB=60°,求∠BOE+∠COF的度数;
(2)若△AEF的周长为8 cm,且BC=4 cm,求△ABC的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com