
【题目】如图所示,在△ABC 中,∠ABC和∠ACB的平分线交于点O,过点O作EF∥BC,交AB于点E,交AC于点F.
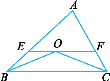
(1)若∠ABC=40°,∠ACB=60°,求∠BOE+∠COF的度数;
(2)若△AEF的周长为8 cm,且BC=4 cm,求△ABC的周长.
【答案】(1)∠BOE+∠COF=50°;(2)12cm.
【解析】
(1)两直线平行,内错角相等,以及根据角平分线性质,可得到![]() 从而求得∠BOE+∠COF的度数.
从而求得∠BOE+∠COF的度数.
(2)根据![]() ,可得△FOC、△EOB均为等腰三角形,由此把△AEF的周长转化为AC+AB,进而可得到△ABC的周长.
,可得△FOC、△EOB均为等腰三角形,由此把△AEF的周长转化为AC+AB,进而可得到△ABC的周长.
解:(1)∵EF∥BC,
∴∠OCB=∠COF,∠OBC=∠BOE.
又∵BO,CO分别是∠BAC和∠ACB的角平分线,
∴∠COF=∠FCO=![]() ∠ACB=30°,∠BOE=∠OBE=
∠ACB=30°,∠BOE=∠OBE=![]() ∠ABC=20°.
∠ABC=20°.
∴∠BOE+∠COF=50°.
(2)∵∠COF=∠FCO,∴OF=CF.
∵∠BOE=∠OBE,∴OE=BE.
∴△AEF的周长=AF+OF+OE+AE=AF+CF+BE+AE=AB+AC=8 cm.
∴△ABC的周长=8+4=12(cm).


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3). 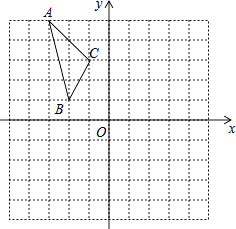
①若△ABC经过平移后得到△A1B1C1 , 已知点C1的坐标为(4,0),写出顶点A1 , B1的坐标;
②若△ABC和△A2B2C2关于原点O成中心对称图形,写出△A2B2C2的各顶点的坐标;
③将△ABC绕着点O按顺时针方向旋转90°得到△A3B3C3 , 写出△A3B3C3的各顶点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
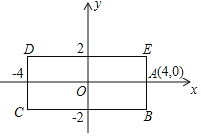
【题目】如图,长方形![]() 的各边分别平行于
的各边分别平行于![]() 轴或
轴或![]() 轴,物体甲和物体乙分别由点
轴,物体甲和物体乙分别由点![]() 同时出发,沿长方形
同时出发,沿长方形![]() 的边作环绕运动.物体甲按逆时针方向以2个单位/秒匀速运动,物体乙按顺时针方向以4个单位/秒匀速运动,则两个物体运动后的第2020次相遇地点的坐标是____.
的边作环绕运动.物体甲按逆时针方向以2个单位/秒匀速运动,物体乙按顺时针方向以4个单位/秒匀速运动,则两个物体运动后的第2020次相遇地点的坐标是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,∠ABC=30°,AC=2,△ABC绕点C顺时针旋转得△A1B1C,当A1落在AB边上时,连接B1B,取BB1的中点D,连接A1D,则A1D的长度是( ) 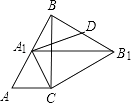
A.![]()
B.2 ![]()
C.3
D.2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图是用4个全等的长方形拼成的一个“回形”正方形,图中阴影部分面积用2种方法表示可得一个等式,这个等式为_______.
(2)若(4x﹣y)2=9,(4x+y)2=169,求xy的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=5,BC=8,D是线段BC上的动点(不含端点B、C).若线段AD长为正整数,则点D的个数共有( )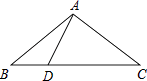
A.5个
B.4个
C.3个
D.2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,(1)∠BED与∠CBE是直线________,________被直线________所截形成的________角;
(2)∠A与∠CED是直线________,________被直线________所截形成的________角;
(3)∠CBE与∠BEC是直线________,________被直线________所截形成的________角;
(4)∠AEB与∠CBE是直线________,________被直线________所截形成的________角.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,△ABC三个顶点的坐标分别为A(﹣2,﹣1),B(﹣4,1),C(﹣3,3).△ABC关于原点O对称的图形是△A1B1C1 . 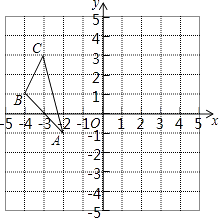
(1)画出△A1B1C1;
(2)BC与B1C1的位置关系是 , AA1的长为;
(3)若点P(a,b)是△ABC 一边上的任意一点,则点P经过上述变换后的对应点P1的坐标可表示为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索:小明在研究数学问题:已知AB∥CD,AB和CD都不经过点P,探索∠P与∠C的数量关系.

发现:在如图中,:∠APC=∠A+∠C;如图
小明是这样证明的:过点P作PQ∥AB
∴∠APQ=∠A(_ __)
∵PQ∥AB,AB∥CD.
∴PQ∥CD(__ _)
∴∠CPQ=∠C
∴∠APQ+∠CPQ=∠A+∠C
即∠APC=∠A+∠C
(1)为小明的证明填上推理的依据;
(2)应用:①在如图中,∠P与∠A、∠C的数量关系为__ _;
②在如图中,若∠A=30![]() ,∠C=70
,∠C=70![]() ,则∠P的度数为__ _;
,则∠P的度数为__ _;
(3)拓展:在如图中,探究∠P与∠A,∠C的数量关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com