
ЁОЬтФПЁПШчЭМЃЌСтаЮABCDЕФБпГЄЮЊ20cmЃЌЁЯABCЃН120ЁуЃЎЖЏЕуPЁЂQЭЌЪБДгЕуAГіЗЂЃЌЦфжаPвд4cm/sЕФЫйЖШЃЌбиAЁњBЁњCЕФТЗЯпЯђЕуCдЫЖЏЃЛQвд2![]() cm/sЕФЫйЖШЃЌбиAЁњCЕФТЗЯпЯђЕуCдЫЖЏЃЎЕБPЁЂQЕНДяжеЕуCЪБЃЌећИідЫЖЏЫцжЎНсЪјЃЌЩшдЫЖЏЪБМфЮЊtУыЃЎ
cm/sЕФЫйЖШЃЌбиAЁњCЕФТЗЯпЯђЕуCдЫЖЏЃЎЕБPЁЂQЕНДяжеЕуCЪБЃЌећИідЫЖЏЫцжЎНсЪјЃЌЩшдЫЖЏЪБМфЮЊtУыЃЎ
ЃЈ1ЃЉдкЕуPЁЂQдЫЖЏЙ§ГЬжаЃЌЧыХаЖЯPQгыЖдНЧЯпACЕФЮЛжУЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ2ЃЉШєЕуQЙигкСтаЮABCDЕФЖдНЧЯпНЛЕуOЕФЖдГЦЕуЮЊMЃЌЙ§ЕуPЧвДЙжБгкABЕФжБЯпlНЛСтаЮABCDЕФБпADЃЈЛђCDЃЉгкЕуNЃЎ
ЂйЕБtЮЊКЮжЕЪБЃЌЕуPЁЂMЁЂNдквЛжБЯпЩЯЃП
ЂкЕБЕуPЁЂMЁЂNВЛдквЛжБЯпЩЯЪБЃЌЪЧЗёДцдкетбљЕФtЃЌЪЙЕУЁїPMNЪЧвдPNЮЊвЛжБНЧБпЕФжБНЧШ§НЧаЮЃПШєДцдкЃЌЧыЧѓГіЫљгаЗћКЯЬѕМўЕФtЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ

ЁОД№АИЁПЃЈ1ЃЉ Шє0ЃМtЁм5ЃЌдђAPЃН4tЃЌAQЃН2t. дђ ЃНЃНЃЌ
гж Ёп AOЃН10ЃЌABЃН20ЃЌЁр ЃНЃН.Ёр ЃНЃЌ
гж ЁЯCABЃН30ЁуЃЌЁр ЁїAPQЁзЁїABOЃЌЁр ЁЯAQPЃН90ЁуЃЌМДPQЁЭAC. ЁЁЁЁЁЁ4Зж
ЕБ5ЉtЁм10ЪБЃЌЭЌРэПЩгЩЁїPCQЁзЁїBCO ПЩЕУЁЯPQCЃН90ЁуЃЌМДPQЁЭACЃЈПМТЧвЛжжЧщПіМДПЩЃЉ
Ёр дкЕуPЁЂQдЫЖЏЙ§ГЬжаЃЌЪМжегаPQЁЭAC.
ЃЈ2ЃЉЂй ШчЭМЃЌдкRtAPMжаЃЌвзжЊAMЃНЃЌгжAQЃН2tЃЌ
QMЃН20Ѓ4t.
гЩAQЃЋQMЃНAM ЕУ2tЃЋ20Ѓ4tЃН
НтЕУtЃНЃЌЁр ЕБtЃНЪБЃЌЕуPЁЂMЁЂNдквЛжБЯпЩЯ. ЁЁЁЁЁЁЁЁЁЁ8Зж
Ђк ДцдкетбљЕФtЃЌЪЙЁїPMNЪЧвдPNЮЊвЛжБНЧБпЕФжБНЧШ§НЧаЮ.
ЩшlНЛACгкH.
ШчЭМ1ЃЌЕБЕуNдкADЩЯЪБЃЌШєPNЁЭMNЃЌдђЁЯNMHЃН30Ёу.
Ёр MHЃН2NHЃЌЕУ 20Ѓ4tЃЃН2ЁС НтЕУtЃН2ЃЌ ЁЁЁЁЁЁЁ10Зж
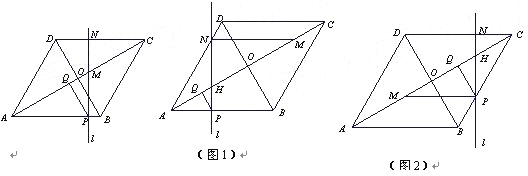
ШчЭМ2ЃЌЕБЕуNдкCDЩЯЪБЃЌШєPMЁЭMNЃЌдђЁЯHMPЃН30Ёу.Ёр MHЃН2PHЃЌЭЌРэПЩЕУtЃН .
ЙЪ ЕБtЃН2Лђ ЪБЃЌДцдквдPNЮЊвЛжБНЧБпЕФжБНЧШ§НЧаЮ. ЁЁЁЁЁЁЁ12Зж
ЁОНтЮіЁП
ЃЈ1ЃЉДЫЮЪашЗжСНжжЧщПіЃЌЕБ0ЃМtЁм5МА5ЃМtЁм10СНВПЗжЗжБ№ЬжТлЕУPQЁЭACЃЎ
ЃЈ2ЃЉЂйгЩгкЕуPЁЂMЁЂNдквЛжБЯпЩЯЃЌдђAQ+QM=AMЃЌДњШыЧѓЕУtЕФжЕЃЎ
ЂкМйЩшДцдкетбљЕФtЃЌЪЙЕУЁїPMNЪЧвдPNЮЊвЛжБНЧБпЕФжБНЧШ§НЧаЮЃЌЕЋЪЧашЗжЕуNдкADЩЯЪБКЭЕуNдкCDЩЯЪБСНжжЧщПіЗжБ№ЬжТлЃЎ
НтД№ЃКНтЃКЃЈ1ЃЉШє0ЃМtЁм5ЃЌдђAP=4tЃЌAQ=2![]() tЃЎ
tЃЎ
дђ![]() =
=![]() =
=![]() ЃЌ
ЃЌ
гжЁпAO=10![]() ЃЌAB=20ЃЌЁр
ЃЌAB=20ЃЌЁр![]() =
=![]() =
=![]() ЃЎ
ЃЎ
Ёр![]() =
=![]() ЃЎгжЁЯCAB=30ЁуЃЌЁрЁїAPQЁзЁїABOЃЎ
ЃЎгжЁЯCAB=30ЁуЃЌЁрЁїAPQЁзЁїABOЃЎ
ЁрЁЯAQP=90ЁуЃЌМДPQЁЭACЃЎ
ЕБ5ЃМtЁм10ЪБЃЌЭЌРэЃЌПЩгЩЁїPCQЁзЁїBCOЕУЁЯPQC=90ЁуЃЌМДPQЁЭACЃЎ
ЁрдкЕуPЁЂQдЫЖЏЙ§ГЬжаЃЌЪМжегаPQЁЭACЃЎ
ЃЈ2ЃЉЂйШчЭМЃЌдкRtЁїAPMжаЃЌЁпЁЯPAM=30ЁуЃЌAP=4tЃЌ
ЁрAM=![]() ЃЎ
ЃЎ
дкЁїAPQжаЃЌЁЯAQP=90ЁуЃЌ
ЁрAQ=AP?cos30Ёу=2![]() tЃЌ
tЃЌ
ЁрQM=AC-2AQ=20![]() -4
-4![]() tЃЎ
tЃЎ
гЩAQ+QM=AMЕУЃК2![]() t+20
t+20![]() -4
-4![]()
t=![]() ЃЌ
ЃЌ
НтЕУt=![]() ЃЎ
ЃЎ
ЁрЕБt=![]() ЪБЃЌЕуPЁЂMЁЂNдквЛжБЯпЩЯЃЎ
ЪБЃЌЕуPЁЂMЁЂNдквЛжБЯпЩЯЃЎ

ЂкДцдкетбљЕФtЃЌЪЙЁїPMNЪЧвдPNЮЊвЛжБНЧБпЕФжБНЧШ§НЧаЮЃЎ
ЩшlНЛACгкHЃЎ
ШчЭМ1ЃЌЕБЕуNдкADЩЯЪБЃЌШєPNЁЭMNЃЌдђЁЯNMH=30ЁуЃЎ
ЁрMH=2NHЃЎЕУ20![]() -4
-4![]() t-
t-![]() t=2ЁС
t=2ЁС![]() ЃЌНтЕУt=2ЃЎ
ЃЌНтЕУt=2ЃЎ
ШчЭМ2ЃЌЕБЕуNдкCDЩЯЪБЃЌШєPMЁЭPNЃЌдђЁЯHMP=30ЁуЃЎ
ЁрMH=2PHЃЌЭЌРэПЩЕУt=![]() ЃЎ
ЃЎ
ЙЪЕБt=2Лђ![]() ЪБЃЌДцдквдPNЮЊвЛжБНЧБпЕФжБНЧШ§НЧаЮЃЎ
ЪБЃЌДцдквдPNЮЊвЛжБНЧБпЕФжБНЧШ§НЧаЮЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖдгкЖўДЮКЏЪ§![]() ЃЎ
ЃЎ
![]() ЫќЕФЭМЯѓгыЖўДЮКЏЪ§
ЫќЕФЭМЯѓгыЖўДЮКЏЪ§![]() ЕФЭМЯѓгаЪВУДЙиЯЕЃПЫќЪЧжсЖдГЦЭМаЮТ№ЃПЫќЕФПЊПкЗНЯђЃЌЖдГЦжсКЭЖЅЕузјБъЗжБ№ЪЧЪВУДЃП
ЕФЭМЯѓгаЪВУДЙиЯЕЃПЫќЪЧжсЖдГЦЭМаЮТ№ЃПЫќЕФПЊПкЗНЯђЃЌЖдГЦжсКЭЖЅЕузјБъЗжБ№ЪЧЪВУДЃП
![]() ЕБ
ЕБ![]() ШЁФФаЉжЕЪБЃЌ
ШЁФФаЉжЕЪБЃЌ![]() ЕФжЕЫц
ЕФжЕЫц![]() ЕФдіДѓЖјдіДѓЃПЕБ
ЕФдіДѓЖјдіДѓЃПЕБ![]() ШЁФФаЉжЕЪБЃЌ
ШЁФФаЉжЕЪБЃЌ![]() ЕФжЕЫц
ЕФжЕЫц![]() ЕФдіДѓЖјМѕаЁЃП
ЕФдіДѓЖјМѕаЁЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙ§ЯпЖЮ![]() ЕФСНЖЫзї
ЕФСНЖЫзї![]() гк
гк![]() ЃЌ
ЃЌ![]() гк
гк![]() ЃЌСЌ
ЃЌСЌ![]() ЁЂ
ЁЂ![]() НЛгк
НЛгк![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌФЧУДЕу
ЃЌФЧУДЕу![]() ЕНЯпЖЮ
ЕНЯпЖЮ![]() ЕФОрРыЮЊ________ЃЎ
ЕФОрРыЮЊ________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() .
.
ЃЈ1ЃЉЕу![]() ЕН
ЕН![]() жсЕФОрРыЮЊЃК______ЃЛ
жсЕФОрРыЮЊЃК______ЃЛ
ЃЈ2ЃЉ![]() ЕФШ§БпГЄЮЊЃК
ЕФШ§БпГЄЮЊЃК![]() ______ЃЌ
______ЃЌ![]() ______ЃЌ
______ЃЌ![]() ______ЃЛ
______ЃЛ
ЃЈ3ЃЉЕБЕу![]() дк
дк![]() жсЩЯЃЌЧв
жсЩЯЃЌЧв![]() ЕФУцЛ§ЮЊ6ЪБЃЌЕу
ЕФУцЛ§ЮЊ6ЪБЃЌЕу![]() ЕФзјБъЮЊЃК______.
ЕФзјБъЮЊЃК______.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
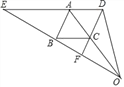
ЁОЬтФПЁП вбжЊЃЌШчЭМБпГЄЮЊ2ЕФе§ЗНаЮABCDжаЃЌЁЯMANЕФСНБпЗжБ№НЛBCЁЂCDБпгкMЁЂNСНЕуЃЌ ЧвЁЯMAN=45.

ЃЈ1ЃЉЧѓжЄЃКMN=BM+DN.
ЃЈ2ЃЉШєAMЁЂANНЛЖдНЧЯпBDгкEЁЂFСНЕуЃЌЩшBF=yЃЌDE=x,ЧѓyгыxЕФКЏЪ§ЙиЯЕЪН.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊDEЁЮBCЃЌAOЃЌDFНЛгкЕуCЃЎЁЯEAB=ЁЯBCFЃЎ
ЃЈ1ЃЉЧѓжЄЃКABЁЮDFЃЛ
ЃЈ2ЃЉЧѓжЄЃКOB2=OEOFЃЛ
ЃЈ3ЃЉСЌНгODЃЌШєЁЯOBC=ЁЯODCЃЌЧѓжЄЃКЫФБпаЮABCDЮЊСтаЮЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
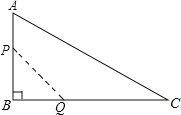
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯB=90ЃЌЁЯC=30ЁуЃЌAB=6cmЃЌBC=6![]() cmЃЌЖЏЕуPДгЕуBПЊЪМбиБпBAЁЂACЯђЕуCвд3cm/sЕФЫйЖШвЦЖЏЃЌЖЏЕуQДгЕуBПЊЪМбиБпBCЯђЕуCвд
cmЃЌЖЏЕуPДгЕуBПЊЪМбиБпBAЁЂACЯђЕуCвд3cm/sЕФЫйЖШвЦЖЏЃЌЖЏЕуQДгЕуBПЊЪМбиБпBCЯђЕуCвд![]() cm/sЕФЫйЖШвЦЖЏЃЌЖЏЕуPЁЂQЭЌЪБГіЗЂЃЌЕНЕуCдЫЖЏНсЪјЃЎЩшдЫЖЏЙ§ГЬжаЁїBPQЕФУцЛ§ЮЊyЃЈcm2ЃЉЃЌдЫЖЏЪБМфЮЊtЃЈsЃЉЃЎ
cm/sЕФЫйЖШвЦЖЏЃЌЖЏЕуPЁЂQЭЌЪБГіЗЂЃЌЕНЕуCдЫЖЏНсЪјЃЎЩшдЫЖЏЙ§ГЬжаЁїBPQЕФУцЛ§ЮЊyЃЈcm2ЃЉЃЌдЫЖЏЪБМфЮЊtЃЈsЃЉЃЎ
ЃЈ1ЃЉЕуPдЫЖЏЕНЕуAЃЌt=ЁЁ ЁЁЃЈsЃЉЃЛ
ЃЈ2ЃЉЧыФугУКЌtЕФЪНзгБэЪОyЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛДЮКЏЪ§![]() ЕФЭМЯёЮЊжБЯп
ЕФЭМЯёЮЊжБЯп![]() ЃЎ
ЃЎ
ЃЈ1ЃЉШєжБЯп![]() гые§БШР§КЏЪ§
гые§БШР§КЏЪ§![]() ЕФЭМЯёЦНааЃЌЧвЙ§ЕуЃЈ0ЃЌ2ЃЉЃЌЧѓжБЯп
ЕФЭМЯёЦНааЃЌЧвЙ§ЕуЃЈ0ЃЌ2ЃЉЃЌЧѓжБЯп![]() ЕФКЏЪ§БэДяЪНЃЛ
ЕФКЏЪ§БэДяЪНЃЛ
ЃЈ2ЃЉШєжБЯп![]() Й§ЕуЃЈ3ЃЌ0ЃЉЃЌЧвгыСНзјБъжсЮЇГЩЕФШ§НЧаЮУцЛ§ЕШгк3ЃЌЧѓ
Й§ЕуЃЈ3ЃЌ0ЃЉЃЌЧвгыСНзјБъжсЮЇГЩЕФШ§НЧаЮУцЛ§ЕШгк3ЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊХзЮяЯпFЃКy=x2+bx+cЕФЭМЯѓОЙ§зјБъдЕуOЃЌЧвгыxжсСэвЛНЛЕуЮЊЃЈЉ![]() ЃЌ0ЃЉЃЎ
ЃЌ0ЃЉЃЎ

ЃЈ1ЃЉЧѓХзЮяЯпFЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌжБЯпlЃКy=![]() x+mЃЈmЃО0ЃЉгыХзЮяЯпFЯрНЛгкЕуAЃЈx1ЃЌy1ЃЉКЭЕуBЃЈx2ЃЌy2ЃЉЃЈЕуAдкЕкЖўЯѓЯоЃЉЃЌЧѓy2Љy1ЕФжЕЃЈгУКЌmЕФЪНзгБэЪОЃЉЃЛ
x+mЃЈmЃО0ЃЉгыХзЮяЯпFЯрНЛгкЕуAЃЈx1ЃЌy1ЃЉКЭЕуBЃЈx2ЃЌy2ЃЉЃЈЕуAдкЕкЖўЯѓЯоЃЉЃЌЧѓy2Љy1ЕФжЕЃЈгУКЌmЕФЪНзгБэЪОЃЉЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉжаЃЌШєm=![]() ЃЌЩшЕуAЁфЪЧЕуAЙигкдЕуOЕФЖдГЦЕуЃЌШчЭМ2ЃЎ
ЃЌЩшЕуAЁфЪЧЕуAЙигкдЕуOЕФЖдГЦЕуЃЌШчЭМ2ЃЎ
ЂйХаЖЯЁїAAЁфBЕФаЮзДЃЌВЂЫЕУїРэгЩЃЛ
ЂкЦНУцФкЪЧЗёДцдкЕуPЃЌЪЙЕУвдЕуAЁЂBЁЂAЁфЁЂPЮЊЖЅЕуЕФЫФБпаЮЪЧСтаЮЃПШєДцдкЃЌЧѓГіЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com