
【题目】如图,函数![]() 的图像与
的图像与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,与函数
,与函数![]() 的图像交于点
的图像交于点![]() ,点
,点![]() 的横坐标为
的横坐标为![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)在![]() 轴上有一动点
轴上有一动点![]() .
.
①若三角形![]() 是以
是以![]() 为底边的等腰三角形,求
为底边的等腰三角形,求![]() 的值;
的值;
②过点![]() 作
作![]() 轴的垂线,分别交函数
轴的垂线,分别交函数![]() 和
和![]() 的图像于点
的图像于点![]() 、
、![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
【答案】(1)A(12,0);(2)a=![]() ;(3)a=6.
;(3)a=6.
【解析】
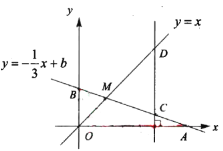
(1)先根据点M在直线y=x上求出M(3,3),把M(3,3)代入![]() 可计算出b=4,得到一次函数的解析式为
可计算出b=4,得到一次函数的解析式为![]() ,然后根据x轴上点的坐标特征可确定A点坐标为(12,0);
,然后根据x轴上点的坐标特征可确定A点坐标为(12,0);
(2)①分别求出PB和PA的长,根据PA=PB列出方程,求出a的值即可;
②先表示出C(a,![]() ),D(a,a),根据CD=2CP列方程求解即可.
),D(a,a),根据CD=2CP列方程求解即可.
(1)∵点![]() 的横坐标为
的横坐标为![]() ,且点M在直线y=x上,
,且点M在直线y=x上,
∴点M的横坐标为3,
∴M(3,3)
把M(3,3)代入![]() 得,
得,![]() ,解得,b=4,
,解得,b=4,
∴![]() ,
,
当y=0时,x=12,
∴A(12,0),
(2)①对于![]() ,当x=0时,y=4,
,当x=0时,y=4,
∴B(0,4),
∵P(a,0),
∴PO=a,AP=12-a,
在Rt△BPO中,![]()
∴![]()
∵PA=PB,
∴![]() ,
,
解得,a=![]() ;
;
②∵P(a,0),
∴C(a,![]() ),D(a,a)
),D(a,a)
∴PC=![]() ,PD=a,
,PD=a,
∴DC=PD-PC=![]() ,
,
∵![]() ,
,
∴![]() =2(
=2(![]() ),
),
解得:a=6.


 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】位于南岸区黄桷垭的文峰塔,有着“平安宝塔”之称.某校数学社团对其高度 AB进行了测量.如图,他们从塔底A的点B出发,沿水平方向行走了13米,到达点C,然后沿斜坡CD继续前进到达点D处,已知DC=BC.在点D处用测角仪测得塔顶A的仰角为42°(点A,B,C,D,E在同一平面内).其中测角仪及其支架DE高度约为0.5米,斜坡CD的坡度(或坡比)i=1:2.4,那么文峰塔的高度AB约为( )(sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)

A. 22.5 米 B. 24.0 米 C. 28.0 米 D. 33.3 米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将等腰△ABC沿对称轴折叠后,得到△ADC(△ADB),若![]() ,则称等腰△ABC为“长月三角形”ABC.
,则称等腰△ABC为“长月三角形”ABC.

(1)结合题目情境,请你判断“长月三角形”一定会是______三角形.
(2)如图2,C为线段AB上一点,分别以AC和BC为边作“长月三角形”ACD和“长月三角形”BCE,连接AE、BD交于点O,AE与CD交于点P,CE与BD交于点M.
①求证:![]() ;
;
②求![]() 的度数.
的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
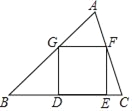
【题目】如图,已知正方形DEFG的顶点D、E在△ABC的边BC上,顶点G、F分别在边AB、AC上,如果BC=5,△ABC的面积是10,那么这个正方形的边长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
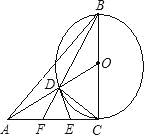
【题目】如图,在△ABC中AC=BC,∠ACB=90°,以BC为直径作⊙O,连接OA,交⊙O于点D,过D点作⊙O的切线交AC于点E,连接B、D并延长交AC于点F.则下列结论错误的是( )
A. △ADE∽△ACO B. △AOC∽△BFC
C. △DEF∽△DOC D. CD2=DFDB
查看答案和解析>>
科目:初中数学 来源: 题型:
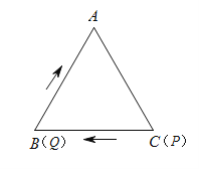
【题目】如图,在等边![]() 中,边长为
中,边长为![]() .点
.点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向运动,速度为
方向运动,速度为![]() ;同时点
;同时点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向运动,速度为
方向运动,速度为![]() ,当两个点有一个点到达终点时,另一个点随之停止运动.设运动时间为
,当两个点有一个点到达终点时,另一个点随之停止运动.设运动时间为![]() ,解答下列问题:
,解答下列问题:
(1)当![]() 时,
时,![]() _______(用含
_______(用含![]() 的代数式表示);
的代数式表示);
(2)当![]() 时,求
时,求![]() 的值,并直接写出此时
的值,并直接写出此时![]() 为什么特殊的三角形?
为什么特殊的三角形?
(3)当![]() ,且
,且![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=﹣x2+bx+c的图象经过坐标原点,且与x轴交于A(﹣2,0).
(1)求此二次函数解析式及顶点B的坐标;
(2)在抛物线上有一点P,满足S△AOP=3,直接写出点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰直角三角形![]() 中,
中,![]() ,
,![]() ,
,![]() .将等腰直角形
.将等腰直角形![]() 沿高
沿高![]() 剪开后,拼成图2所示的正方形
剪开后,拼成图2所示的正方形![]() .
.
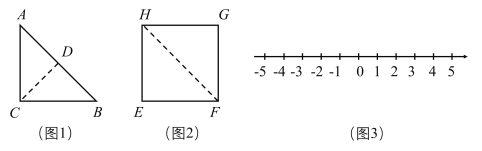
(1)如图1,等腰直角三角形![]() 的面积是______________.
的面积是______________.
(2)如图2,求正方形![]() 的边长是多少?
的边长是多少?
(3)把正方形![]() 放到数轴上(如图3),使得边
放到数轴上(如图3),使得边![]() 落到数轴上,其中一个端点所对应的数为-1,直接写出另一个端点所对应的数.
落到数轴上,其中一个端点所对应的数为-1,直接写出另一个端点所对应的数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com