
【题目】如图,C、F在BE上,∠A=∠D,AC∥DF,BF=EC.你知道AB与DE有什么关系?请说明理由.

【答案】AB=DE且AB∥DE,理由详见解析.
【解析】
试题分析:先求出BC=EF,根据两直线平行,内错角相等可得∠ACF=∠DFC,再根据等角的补角相等求出∠ACB=∠DFE,然后利用“角角边”证明△ABC和△DEF全等,根据全等三角形对应边相等可得AB=DE,全等三角形对应角相等可得∠B=∠E,再根据内错角相等,两直线平行可得AB∥DE.
试题解析:AB=DE且AB∥DE.
理由如下:∵BF=EC,
∴BF﹣CF=EC﹣CF,即BC=EF,
∵AC∥DF,
∴∠ACF=∠DFC,
∴180°﹣∠ACF=180°﹣∠DFC,
即∠ACB=∠DFE,
在△ABC和△DEF中,
∠A=∠D,∠ACB=∠DFE,BC=EF,
∴△ABC≌△DEF,
∴AB=DE,∠B=∠E,
∴AB∥DE,
综上所述,AB与DE的关系是AB=DE且AB∥DE.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,EF//AD,∠1=∠2,∠BAC=70°,请将求∠AGD 的过程补充完整.

解:∵EF//AD
∴∠2= ( )
∵∠1=∠2 ∴∠1=∠3 ( )
∴AB// ![]() ( )
( )
∴∠BAC+ =180° ( )
∵∠BAC=70° ∴∠AGD= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)经过A,B,C三点,点B的坐标为(-3,0),且OC=3OA,直线y=x+m经过B、C两点.
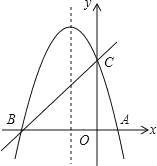
(1)求抛物线的解析式;
(2)在抛物线的对称轴上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;
(3)设点P为抛物线的对称轴上的一个动点,求使△BPC为直角三角形的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算x(x2-1)+2x2(x+1)-3x(2x-5)的结果是( )
A. 3x3-4x2+14xB. 3x3-4x2+14xC. 3x3-4x2+14xD. 3x3-4x2+14x
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com