Question

【题目】如图，已知抛物线y=ax2+bx+c（a≠0）经过A，B，C三点，点B的坐标为（-3，0），且OC=3OA，直线y=x+m经过B、C两点．

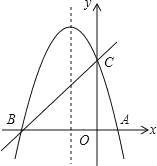
（1）求抛物线的解析式；

（2）在抛物线的对称轴上找一点M，使点M到点A的距离与到点C的距离之和最小，求出点M的坐标；

（3）设点P为抛物线的对称轴上的一个动点，求使△BPC为直角三角形的点P的坐标．

Answer 1

【答案】（1）y=-x2-2x+3；（2）（-1，2）；（3）（-1，-2）或（-1，4）或（-1，）或（-1，）．

【解析】

试题分析：（1）先把点B代入y=x+m，求得m的值，求得C的坐标，然后根据待定系数法即可求得抛物线的解析式；

（2）设直线BC与对称轴x=-1的交点为M，则此时MA+MC的值最小．把x=-1代入直线y=x+3得y的值，即可求出点M坐标；

（3）设P（-1，t），又因为B（-3，0），C（0，3），所以可得BC2=18，PB2=（-1+3）2+t2=4+t2，PC2=（-1）2+（t-3）2=t2-6t+10，再分三种情况分别讨论求出符合题意t值，即可求出点P的坐标．

试题解析：（1）把B（-3，0）代入y=x+m，

得-3+m=0，m=3，

∴直线的解析式为y=x+3；

∴点C的坐标为（0，3），

∵OC=3OA，

∴点A的坐标为（1，0），

∴，解得，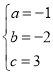

∴抛物线的解析式为y=-x2-2x+3；

（2）∵y=-x2-2x+3=-（x+1）2+4，

∴对称轴是直线x=-1，

设直线BC与对称轴x=-1的交点为M，则此时MA+MC的值最小．

把x=-1代入直线y=x+3得，y=2，

∴M（-1，2），

即当点M到点A的距离与到点C的距离之和最小时M的坐标为（-1，2）；

（3）设P（-1，t），又∵B（-3，0），C（0，3），

∴BC2=18，PB2=（-1+3）2+t2=4+t2，PC2=（-1）2+（t-3）2=t2-6t+10，

①若点B为直角顶点，则BC2+PB2=PC2

即：18+4+t2=t2-6t+10解之得：t=-2；

②若点C为直角顶点，则BC2+PC2=PB2

即：18+t2-6t+10=4+t2解之得：t=4，

③若点P为直角顶点，则PB2+PC2=BC2

即：4+t2+t2-6t+10=18解之得：t1=，t2=；

综上所述P的坐标为（-1，-2）或（-1，4）或（-1，）或（-1，）．